Методико-практический путеводитель по темам курса "Теория статистики", страница 18

Аналогично вычисленные внутригрупповые дисперсии для второй и третьей групп:  = 0,06. Средняя из групповых дисперсий

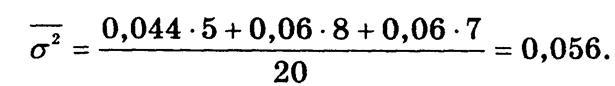
Межгрупповая дисперсия составляет

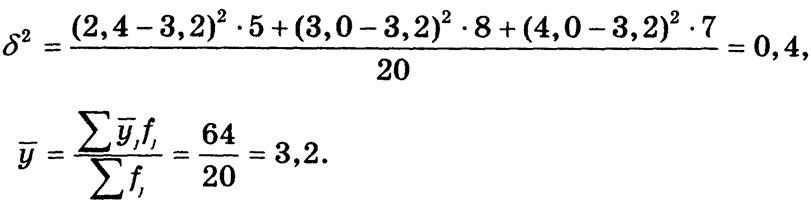
Общую дисперсию урожайности определим по правилу разложения дисперсий как сумму межгрупповой и средней из групповых дисперсий:

s² = 0,4 + 0,056 = 0,456

Непосредственное вычисление общей дисперсий по упрощенной формуле

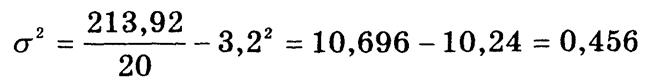
дает тот же результат.

5. Выборочный метод. Статистическая проверка гипотез

Выборочный метод — это система научных принципов случайного отбора определенной части совокупности, которая представляла бы всю совокупность и характеристики которой служили бы надежной основой статистического вывода.

Совокупность, из которой отбираются элементы для обследования, называют генеральной, а совокупность, которую непосредственно обследуют, — выборочной. Статистические характеристики выборочной совокупности рассматриваются как оценки соответствующих характеристик генеральной совокупности. Поскольку выборочная совокупность неточно воспроизводит структуру генеральной, то выборочные оценки также не совпадают с характеристиками генеральной совокупности. Различия между ними называют ошибками репрезентативности. По причинам появления эти ошибки делятся на систематические (тенденционные) и случайные. Систематические ошибки появляются, если при формировании выборочной совокупности нарушен принцип случайности отбора (преднамеренный отбор элементов, несовершенная основа выборки и т. п.). Случайные ошибки — это следствие случайности отбора элементов совокупности для обследования.

При организации выборочного обследования важно предупредить появление систематических ошибок. Избежать случайных ошибок невозможно, однако на основе теории выборочного метода можно определить их размер и по возможности регулировать.

В практике выборочных наблюдений используют два типа выборочных оценок — точечные и интервальные. Точечная оценка — это значение параметра по данным выборки: выборочная средняя  или выборочная доля р. Интервальная оценка — это интервал значений параметра, рассчитанный по данным выборки для определенной вероятности, т. е. доверительный интервал. Границы его определяются на основе точечной оценки и предельной ошибки выборки D = tm:

для средней

для доли

где m — средняя, или стандартная ошибка выборки; t — квантиль распределения вероятностей (доверительное число);  и d₀ — средняя и доля в генеральной совокупности.

Стандартная ошибка выборки m является средним квадратическим отклонением выборочных оценок от значений параметра, генеральной совокупности:

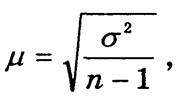
при повторном отборе

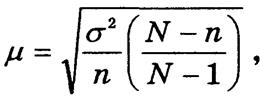
при бесповторном

где s² — выборочная дисперсия; n и N — соответственно объем выборочной и генеральной совокупностей.

При практическом использовании данных формул следует учитывать, что:

1) дисперсия альтернативного признака рассчитывается как произведение долей s² = р(1 - р) = pq;

2) в больших по объему совокупностях (30 и более единиц) поправка  не вносит существенных изменений в расчеты, а поэтому учитывается только в малочисленных (малых) выборках;

3) корректирующий множитель для бесповторной выборки 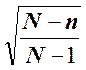при малых величинах  приближается к 1, поэтому при 1—5%-й выборке расчет m проводится по формуле для повторной выборки.

Предельная ошибка выборки D = tm — это максимально возможная ошибка для принятой вероятности F(x). Доверительное число t показывает, как соотносятся предельная и стандартная ошибки. Так, t = 1 для вероятности 0,683; t = 2 для вероятности 0,954; t = 3 для вероятности 0,997.

Таким образом, используют следующие формулы предельной ошибки выборки:

Как видно из формул, размер предельной ошибки зависит от вариации признака s², объема выборки n и ее доли в генеральной совокупности , а также принятого уровня вероятности, которому соответствует квантиль t.