Методико-практический путеводитель по темам курса "Теория статистики", страница 21

Примером стохастической, и в частности корреляционной, связи является распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости у и размеру общей площади х (табл. 6.1).

Таблица 6.1

Размер общей площади, м2 х	Количество квартир со стоимостью тыс. усл. ден. ед.						Средняя стоимость квартиры, тыс. усл. ден. ед.
	9—11	11—13	13—15	15—17	17—19	Итого fi
До 25	26	12	2	—	—	40	10,8
25-30	4	9	12	5	—	30	13,2
30-35	—	4	6	10	4	24	15,2
35 и более	—	—	—	—	6	6	18,0
В целом	30	25	20	15	10	100	13,0

Каждой группе по факторному признаку соответствует свое распределение y, отличающееся от других групп и от безусловного итогового распределения. Следовательно, между признаками наблюдается стохастическая связь.

Условные распределения можно заменить средними значениями результативного признака, вычисляемыми как средняя арифметическая взвешенная:

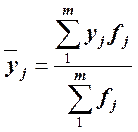
Постепенное изменение средних  от одной группы к другой свидетельствует о наличии корреляционной связи между признаками.

Характеристикой корреляционной связи является линии регрессии, которая рассматривается в двух моделях: аналитической группировки и регрессионного анализа. В модели аналитической группировки — это эмпирическая линия регрессии, которая образуется из групповых средних значений результативного признака  для каждого значения (интервала) х_о.

Эффекты, воздействия х на у определяются как отношение приростов средних групповых значений D_y : D_x, где ,  По данным табл. 6.1 приросты D_x во всех группах одинаковы — 5 м², а средняя стоимость проданных квартир увеличивается по группам таким образом:  = 13,2 - 10,8 = 2,4 тыс. усл. ден. ед.;  = 2,0;  = 2,8.

Следовательно, с увеличением размера общей площади квартир на 1 м² их стоимость в среднем возрастает соответственно на:  :  = 2,4 : 5 == 0,48; на 0,4 и 0,56 тыс. усл. ден. ед.

Оценка тесноты связи основывается на правиле сложения дисперсий. В модели аналитической группировки мерой тесноты является отношение межгрупповой дисперсии к общей, которое называют корреляционным отношением:

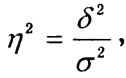
где s² — общая дисперсия, измеряющая вариацию результативного признака у, обусловленную влиянием всех возможных факторов; межгрупповая дисперсия d² измеряет вариацию результативного признака у за счет воздействия только группировочного признака х. Корреляционное отношение колеблется в пределах от 0 до 1 (или от 0 до 100%). При функциональной связи h² = 1, если связь отсутствует — h² = 0. Чем ближе h² к единице, тем теснее связь.

По данным табл. 6.1, общая дисперсия стоимости проданных квартир составляет

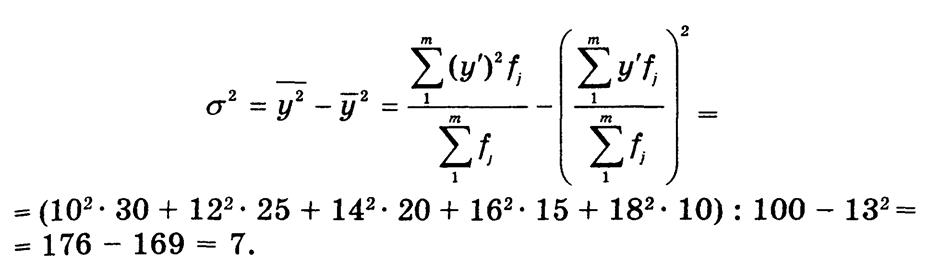
В табл. 6.2 представлена аналитическая группировка проданных квартир, описывающая зависимость их стоимости от общей площади. Там же показан расчет межгрупповой дисперсии.

Таблица 6.2

Общая площадь квартиры, м2	Количество квартир	Средняя стоимость квартиры, тыс. усл. ден. ед.
xi	fi
До 25	40	10,8	-2,2	193,6
25—30	30	13,2	0,2	1,2
30—35	24	15,2	2,2	116,2
35 и более	6	18,0	5,0	150,0
В целом	100	13,0	X	461,0

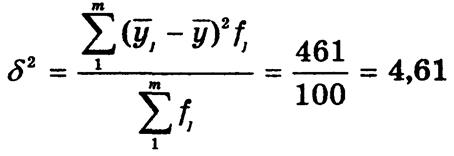
Корреляционное отношение составляет:

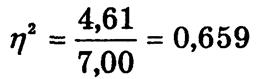
следовательно, вариация стоимости проданных квартир на 66% объясняется вариацией их общей площади и на 34% — вариацией других факторов. Таким образом, связь между признаками достаточно тесная.