Соотношения между отдельными составляющими совокупности являются относительными величинами координации. Они показывают, сколько единиц одной части совокупности приходится на 1 или 100 единиц другой, принятой за базу сравнения. Выбор базы сравнения произвольный. Например, на начало года капитал фирмы составлял 400 млн ден. ед., из них собственный капитал — 260 млн ден. ед., привлеченный — 140. Доля собственного капитала составляет 260 : 400 = 0,65, доля привлеченного капитала — 140 : 400 = 0,35. Сумма долей равна 0,65 + 0,35 = 1. Соотношение собственного и привлеченного капитала показывает, что на 100 ден. ед. собственного капитала приходится 54 ден. ед. привлеченного.
По соотношению абсолютных величин, представленных в форме балансов, оценивают сбалансированность процессов. Например, сбалансированность доходов и расходов населения, сбалансированность экспортно-импортных операций и т. п.
Средняя величина — это обобщающая мера варьирующего признака, которая характеризует его уровень в расчете на единицу совокупности. Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой ее объем.
В статистической практике используют несколько видов средних, средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т. д. Каждая из названных средних может иметь две формы: простую и взвешенную. Если средняя вычисляется по первичным (несгруппированным) данным, применяется простая форма, если по вторичным (сгруппированным) — взвешенная.
Использование каждого вида средних зависит от двух обстоятельств: во-первых, от характера индивидуальных значений признака (прямые, обратные, квадратические, относительные); во-вторых, от характера алгебраической связи между индивидуальными значениями признака и его общим объемом (сумма, произведение, степень, квадратный корень. Эта связь является определяющим свойством совокупности и отражается в логической формуле осредняемого признака. Логическая формула предопределяет вид средней.
Средняя арифметическая используется для осреднения прямых значений признаков путем их суммирования. логическая формула имеет вид
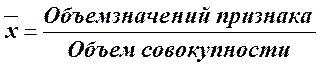
Если данные не сгруппированы, применяется средняя арифметическая простая
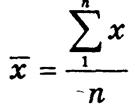
где х — отдельные значения признака; n — объем совокупности.
Пример. Уставной фонд акционерной компании сформирован 6 учредителями; размер взноса каждого из них составляет, млн ден. ед.: 6; 10; 12; 9; 7; 4. Средний взнос одного учредителя
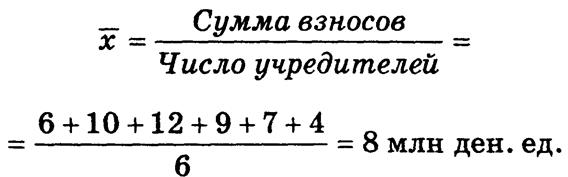
По формуле средней арифметической простой вычисляются также средние в хронологическом ряду, если интервалы времени, за которое приводятся значения признаков, равны.
Пример. Квартальный оборот универсальных бирж в течение года составлял, млн ден. ед.: I кв. — 372; II кв. — 423;
III кв. — 340; IV кв. — 455. Среднеквартальный оборот бирж составляет

Если в хронологическом ряду приведены моментные показатели, то для вычисления средней они заменяются полусуммами значений на начало и конец периода. Если моментов более двух и интервалы между ними равны, то средняя вычисляется по формуле средней хронологической простой
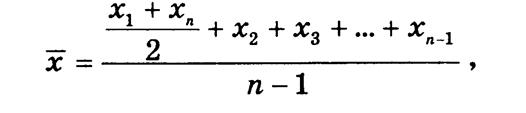
где n — число моментов.
Пример. В коммерческом банке сумма кредиторской задолженности на начало каждого квартала составляла, млн ден. ед.: 01.01 — 20; 01.04 — 26; 01.07 — 32; 01.10 — 29; 01.01 следующего года — 22. Среднеквартальная сумма кредиторской задолженности
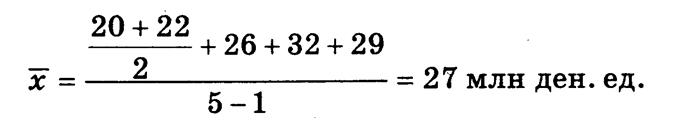
Если данные сгруппированы, то используют средневзвешенную арифметическую
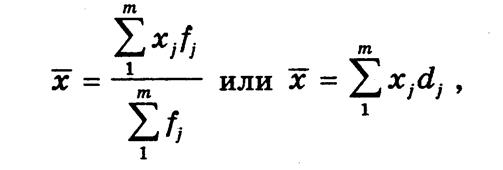
где fj — частота; dj — частость j-й группы. При этом
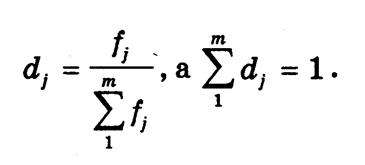
Так, по результатам сдачи экзамена студентами группы (табл. 3.1), средний балл оценок составляет 3,8.
Таблица 3.1
|
Оценка знаний студентов, балл |
xi |
5 |
4 |
3 |
2 |
Итого |
|
Количество оценок |
fi |
8 |
12 |
6 |
4 |
30 |
|
Доля оценок |
di, |
0,267 |
0,400 |
0,200 |
0,133 |
1,00 |
На основе частот
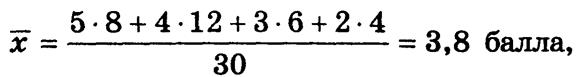
![]() на
основе частостей
на
основе частостей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.