Методико-практический путеводитель по темам курса "Теория статистики", страница 26

Темп прироста Т_t показывает, на сколько процентов уровень у_t больше (меньше) уровня, принятого за базу сравнения. Его можно определить либо через отношение абсолютного прироста к базе сравнения, либо непосредственно на основе темпа роста. Так, для цепных характеристик:

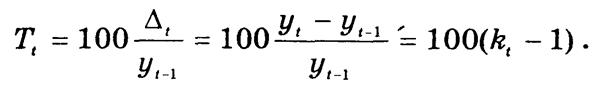
Аналогично взаимосвязаны и базисные характеристики динамики.

Абсолютное значение 1% прироста рассчитывается как соотношение абсолютного прироста и темпа прироста. Алгебраически это соотношение равно 0,01 уровня, принятого за базу сравнения:

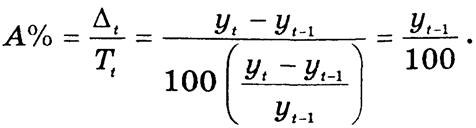
Для базисных темпов прироста значения А% одинаковы. Порядок расчета характеристик динамики рассмотрим на примере изменения объема экспорта товаров (табл. 7.2).

За II—IV кварталы экспорт товаров увеличился на 1,4 млрд дол. США, или на 50% по сравнению с I кварталом. Поквартальные абсолютные приросты и темп прироста снижались, однако абсолютное значение 1% прироста увеличивалось.

Таблица 7.2

Квартал	Объем экспорта, млрд дол. США	Абсолютный прирост, млрд дол. США		Темп роста, %		Темп прироста, %		Абсолютное значение 1% прироста, млн дол. США
		цепной	базисный	цепной	базисный	цепной	базисный
I	2,8	—	—	—	100	—	—	—
II	3,5	0,7	0,7	125	125	25	25	28
III	3,9	0,4	1,1	111	139	11	39	35
IV	4,2	0,3	1,4	108	150	8	50	39

Обобщающими характеристиками интенсивности динамики являются средний абсолютный прирост  и средний темп роста . Средний абсолютный прирост рассчитывается как средняя арифметическая простая из цепных абсолютных приростов:

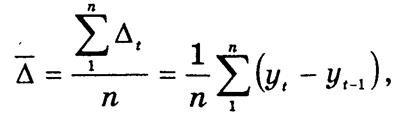
где n — число цепных абсолютных приростов.

Средний темп роста вычисляют по формуле средней геометрической:

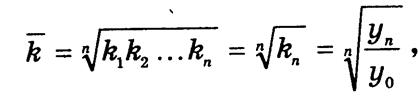
где n — число цепных темпов роста.

По данным табл. 7.2  = 1,4 : 3 = 0,46 млрд дол. США, , т.е. объем экспорта товаров ежеквартально возрастал в среднем на 460 млн дол. США, или на 14,5%.

Если абсолютная или относительная скорость динамики в пределах изучаемого периода неодинакова, то ускорение (замедление) динамики измеряется путем сравнения одноименных характеристик за разные интервалы времени. Разность абсолютных цепных приростов D’ = D_t - D_t-1 характеризует абсолютное ускорение (+) или замедление (-) динамики. Для положительных абсолютных приростов можно определить относительное ускорение (D_t / D_t-1). Если интервалы времени неодинаковы, используют средние абсолютные приросты за соответствующие периоды.

На основе темпов роста (базисных или средних) проводят сравнительный анализ интенсивности динамики параллельных рядов, например грузооборота железнодорожного и автомобильного транспорта. Соотношение темпов роста различных объектов называют коэффициентом опережения.

Если ряды динамики взаимосвязаны, т. е. уровни их рассматриваются как фактор х и результат y, соотношение темпов прироста этих признаков позволяет определить, на сколько процентов изменяется у при изменении х на 1%. По содержанию соотношение темпов прироста является коэффициентом эластичности k_эл = Т_у / Т_х. Например, цены на товар выросли на 5%, а спрос уменьшился на 3%. Темпы прироста цен и снижения спроса составляют соответственно Т_у = -3%, Т_х = -5%. Следовательно, k_эл = -3/5 = -0,6, т.е. с увеличением цен на 1 % спрос уменьшается на 0,6%.

Предпосылкой анализа динамических рядов? является сопоставимость данных, которая обеспечивается на этапах их сбора и обработки. Однако возможна ситуация, когда изменения в методологии расчета показателя, структурные сдвиги, изменение цен и т.п. приводят к тому, что данные оказываются несопоставимыми. В таких случаях исполосуют специальные приемы смыкания прерывистых рядов — "статистические ключи". Например, дан прерывистый ряд: