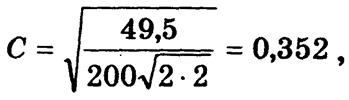
т.е. связь между признаками умеренная.
В случае, когда mx = my = 2, расчет коэффициента взаимной сопряженности упрощается:
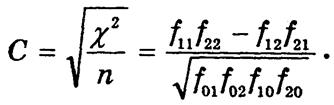
В статистической литературе коэффициент С для 4-клеточной таблицы называют коэффициентом контингенции (ассоциации). Очевидно, что c2 = nС2.
Для анализа таблиц такого типа используют также отношение перекрестных произведений, или отношение шансов:
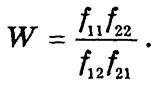
Отношение шансов характеризует меру относительного риска (выигрыша), связанного с фактором х.
Пример. По данным табл. 6.6 оценим тесноту связи между восприятием рекламы и приобретением рекламируемого товара, а также результативность рекламы.
Таблица 6.6
|
Восприятие рекламы |
Количество респондентов |
Итого |
|
|
приобрели товар |
не приобрели товар |
||
|
Запомнили рекламу |
9 |
31 |
40 |
|
Не запомнили рекламу |
2 |
38 |
40 |
|
Итого |
11 |
69 |
80 |
Коэффициент контингенции свидетельствует о наличии стохастической связи
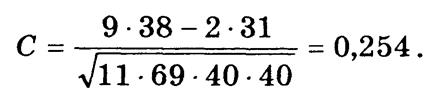
фактическое значение c2 = nС2 = 80 • 0,2542 = 5,16, что выше критического значения c20,95(1) = 3,84. Следовательно, существенность связи доказана.
Отношение шансов составляет
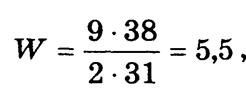
т.е. шансы реализовать рекламируемый товар в 5,5 рааза выше по сравнению с нерекламируемым.
Методы анализа таблиц взаимной сопряженности можно использовать и для количественных признаков (см., например, комбинационное распределение табл. 6.1), однако следует отметить, что меры тесноты корреляционной связи – коэффициент детерминации и корреляционное отношение – более чувствительны.
Динамический ряд — это расположенные в хронологической последовательности значения определенного статистического показателя. Составляющими динамического ряда являются признак времени t (момент или интервал) и числовые значения показателя — уровни уt. В зависимости от типа показателей по признаку времени выделяют моментные и интервальные ряды динамики. В моментных рядах уровни фиксируют состояние явления на определенные моменты времени, в интервальных — агрегированный результат за определенный промежуток времени. Примеры указанных рядов динамики приведены в табл. 7.1: поквартальные объемы экспорта товаров образуют интервальный ряд, суммы резервов иностранной валюты на конец квартала — моментный.
Таблица 7.1
|
Год, квартал |
Объем экспорта товаров в ценах ФОБ, млрд дол. США |
Сумма резервов иностранной валюты на конец квартала, млрд дол. США |
|
1998 IV |
— |
4,7 |
|
1999 I |
2,8 |
6,3 |
|
II |
3,5 |
14,1 |
|
III |
3,9 |
9,9 |
|
IV |
4,2 |
9,1 |
Уровни рядов динамики изменяются, варьируют. Обобщающей их характеристикой является средний уровень, который для интервального ряда рассчитывается по формуле средней арифметической простой, а для моментного — по формуле средней хронологической. По данным табл. 7.1 среднеквартальный объем экспорта товаров составляет
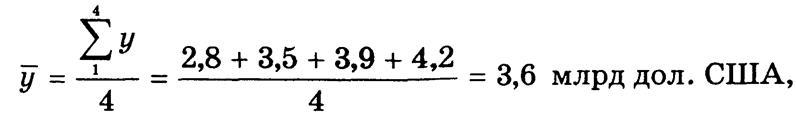
а среднеквартальный резерв иностранной валюты
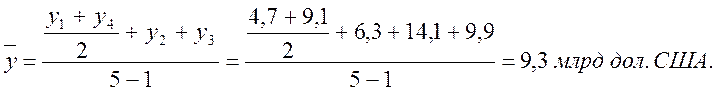
При изучении особенностей развития социально-экономических явлений используют абсолютные и относительные характеристики динамики: абсолютный прирост и абсолютное значение 1% прироста; темп роста (индекс) и темп прироста. Расчет их основывается на сравнении уровней динамического ряда. Если база сравнения постоянная, характеристики динамики называют базисными, если база сравнения переменная — цепными.
Абсолютный прирост (снижение) Dt — это разность уровней динамического ряда:
цепные Dt = yt – уt-1,
базисные Dt = yt – у0.
Очевидно, что сумма цепных абсолютных приростов равна конечному базисному:
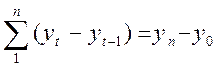
Темп роста k^ рассчитывается как отношение уровней ряда и может быть выражен с помощью коэффициентов или в процентах:
цепные
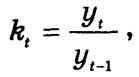
базисные
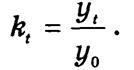
Произведение цепных kt равно конечному базисному:
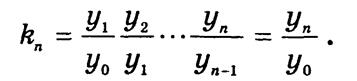
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.