Методико-практический путеводитель по темам курса "Теория статистики", страница 14

Показатель	Уровень показателя хij	Норматив xi.st	pij
Рентабельность активов, %	47,20	20,00	2,36
Оборотность активов, %	0,80	0,67	1,19
Коэффициент капитализации, %	3,90	<10,00	2,56
Коэффициент задолженности	0,34	0,70	2,06
Итого	X	X	8,17

Многомерная средняя составляет = 8,17 : 4 = 2,04, т. е. финансовое состояние эмитента можно считать привлекательным для инвесторов.

4. Ряды распределения. Анализ вариаций и формы распределения

Ряд распределения характеризует состав и структуру совокупности по определенному признаку. Элементами ряда распределения являются варианты — значения признака х_j и частоты f_j. В зависимости от статистической природы вариантов ряды делятся на атрибутивные и вариационные. В соотношении вариантов и частот проявляется закономерность распределения. Она описывается различными статистическими характеристиками, среди которых:

а) частотные характеристики;

б) характеристики центра распределения;

в) характеристики вариации;

г) характеристики неравномерности распределения, концентрации, асимметрии.

Частотными характеристиками любого ряда распределения являются абсолютная численность j-й группы — частота f_j и относительная частота — частость d_j.

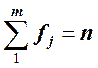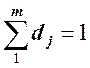Очевидно, что , a  или 100%.

Дополнительная характеристика вариационных рядов — кумулятивная частота S_f (частость S_d), которая характеризует объем совокупности со значениями вариантов, не превышающими х_j. Кумулятивные частотные характеристики образуются последовательным суммированием абсолютных или относительных частот. Так, S₁ = f₁, S₂ = f₁+ f₂, S₃ = f₁ + f₂ + f₃ и т. д. Если интервалы вариационного ряда неравные, то используют плотность частоты (частости) на единицу интервала g_j = f_j : h_j или g_j = d_j : h_j, где h_j — величина j-го интервала.

К характеристикам центра распределения относят среднюю, моду и медиану. Средняя величина характеризует типичный уровень признака в совокупности. По данным ряда распределения средняя рассчитывается как арифметическая взвешенная:

на основе частот

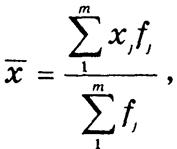
на основе частостей

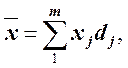
где m — число групп.

В интервальных рядах, допуская, что распределение в границах j-го интервала является равномерным, как вариант х_j используют середину интервала. При этом величину открытого интервала условно считают такой же, как и величину соседнего закрытого интервала. Так, в ряду распределения, характеризующем спрос на гособлигации на вторичном рынке (табл. 4.1), средний срок обращения облигаций составляет

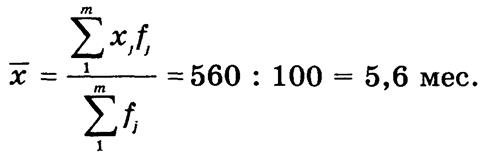
Мода Мо — это наиболее распространенное значение признака, т.е. вариант, который в ряду распределения имеет наибольшую частоту (частость).

В дискретном ряду Мо определяется визуально по максимальной частоте или частости. Например, по данным самооценки материального состояния населения по четырем градациям (хороший, удовлетворительный, неудовлетворительный, невыносимый) большинство респондентов определили свое состояние как неудовлетворительное. Другой пример: в распределении современных семей по количеству детей наиболее распространенными являются малодетные семьи, которые имеют 1 ребенка.

Встречаются ряды, имеющие две моды (бимодальный ряд) или несколько (полимодальный). Например, на фондовом рынке одинаково высоким спросом пользуются как самые дешевые акции, так и дорогие. В интервальном ряду по наибольшей частоте определяется модальный интервал. Конкретное значение моды в интервале вычисляется по формуле

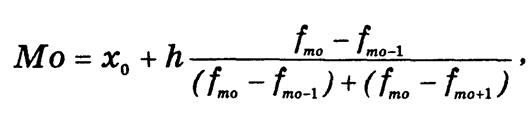
где х₀ и h — соответственно нижняя граница и величина модального интервала; f_mo, f_mo-1, f_mo+1 — частоты (частости) модального, предмодального и послемодального интервалов.

По данным табл. 4.1, наибольшим спросом пользуются акции со сроком обращения в интервале 4—6 месяцев. Это модальный интервал, ширина которого h = 2, а нижняя граница x₀ = 4, частота f_mo = 29, предмодальная частота f_mo-1 = 13, а послемодальная f_mo+1 = 22. Модальный срок обращения облигаций составляет