Математика \ Теория статистики

Методико-практический путеводитель по темам курса "Теория статистики", страница 17

% к итогу

Стоимость реализованной продукции, тыс. ден. ед.

Количество ферм,

di

Стоимость реализованной продукции

Di

До 2

12

2

0,17

10

2—5

28

8

0,28

20

5—10

31

16

0,52

15

10—20

17

19

1,12

2

20—40

8

23

2,87

15

40 и более

4

32

8,00

28

Итого

100

100

X

90

Коэффициенты концентрации и локализации являются эффективным средством измерения дифференциации совокупности по данным интервальных рядов с неравными интервалами и по данным атрибутивных рядов. По аналогии с коэффициентом концентрации рассчитывают коэффициент подобия (сходства) структур двух объектов или одного объекта по двум признакам:

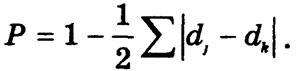
Если структуры одинаковы, Р = 1. Чем больше отклонения структур, тем меньше значения коэффициента Р.

Для оценки интенсивности структурных сдвигов во времени используют абсолютные меры вариации — среднее линейное или среднее квадратическое отклонение частостей, которые называют коэффициентами структурных сдвигов:

линейный

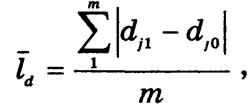
квадратический

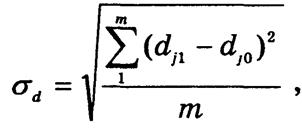
где dj0 и dj1 — частости распределения за два периода; m — число составляющих совокупности.

Пример расчета линейного коэффициента структурных сдвигов в промышленном потреблении алюминия приведен в табл. 4.4. По данным таблицы

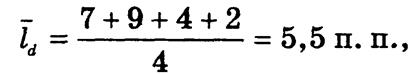
т.е. структура промышленного потребления алюминия изменилась в среднем на 5,5 процентного пункта.

Таблица 4.4

Отрасль потребления алюминия

% к итогу

Структурные сдвиги, процентные пункты

1985 г.

1995 г.

Транспортное машиностроение

33

26

-7

Производство тары и упаковки

20

29

9

Производство товаров долгосрочного пользования

13

9

-4

Другое

34

36

2

Итого

100

100

0

Дисперсия, в отличие от других характеристик вариации, является аддитивной величиной. То есть в структурированной совокупности, разделенной на группы по признаку х, дисперсия признака у может быть разложена на: дисперсию в каждой группе (внутригрупповую) и дисперсию между группами (межгрупповую). Общая дисперсия характеризует вариацию признака у в целом по совокупности, межгрупповая — вариацию групповых средних, а внутригрупповые — вариацию индивидуальных значений относительно групповых средних.

Межгрупповая дисперсия вычисляется по формуле

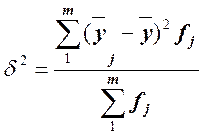
где  и  — соответственно средняя j-й группы и общая средняя варьирующего признака у; fj — частота j-й группы.

Внутригрупповая дисперсия рассчитывается отдельно для каждой j-й группы:

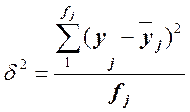
где у — значение признака у отдельных элементов совокупности.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп:

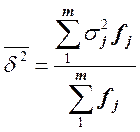
Взаимосвязь между тремя дисперсиями получил название правила сложения дисперсий, в соответствии с которым

Общую дисперсию можно определить и непосредственно по формуле

Отношение межгрупповой дисперсии к общей называется корреляционным отношением, h2.

Расчет указанных дисперсий показан в табл. 4.5 на примере вариации урожайности винограда.

Вариация урожайности отдельно для каждого сорта винограда определяется тремя внутригрупповыми дисперсиями. Для сорта винограда "Алиготе" внутригрупповая дисперсия составляет

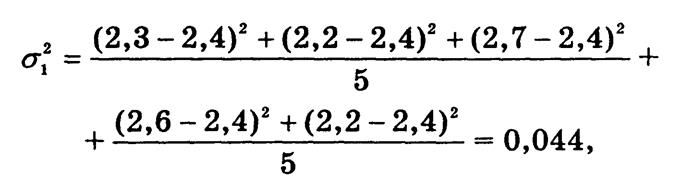
где

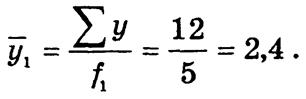
Таблица 4.5

Сорт винограда

Количество кустов

Урожайность с одного куста, кг

Sy

fi

y

Алиготе

5

2,3; 2,2; 2,7; 2,6; 2,2

12

2,4

Фетяска

8

2,9; 3,3; 2,7; 2,8; 3,2;

3,4; 2,8; 2,9

24

3,0

Рислинг

7

3,6; 4,0; 4,1; 4,4; 3,8;
3,9; 4,2

28

4,0

В целом

20

X

64

3,2
Скачать файл