Методико-практический путеводитель по темам курса "Теория статистики", страница 15

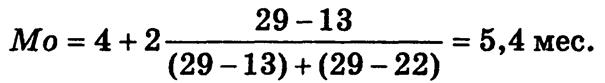
Таблица 4.1

Срок обращения, мес.	Количество проданных государственных облигаций, тыс.	Кумулятивная частота, тыс.
х	fj	Sf	xj	xjfj
До 2	15	15	1	15
2—4	13	28	3	39
4—6	29	57	5	145
6—8	22	79	7	154
8—10	12	91	9	108
10 и более	9	100	11	99
Итого	100	X	X	560

Медиана Me — это вариант, который расположен в середине упорядоченного ряда распределения и делит его на две равные по объему части. Медиана, как и мода, не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами. Для определения Me в ряду используют кумулятивные частоты S_f или частости S_d. В дискретном ряду медианой будет значение признака, для которого кумулятивная частота S_f равна или превышает половину объема совокупности 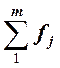, или кумулятивная частость S_d > 0,5. В интервальном ряду таким образом определяется медианный интервал. Конкретное значение медианы в интервале вычисляется по формуле

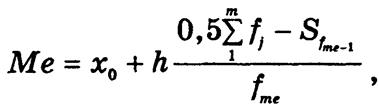
где x₀ и h — соответственно нижняя граница и величина медианного интервала; f_me — частота медианного интервала;  — кумулятивная частота предмедианного интервала. До данным табл. 4.1, половина объема совокупности проданных облигаций

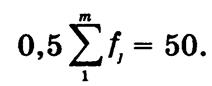
Следовательно, кумулятивная частота   = 57 определяет, что пятидесятая с начала ряда облигация будет находиться в интервале 4—6 с частотой f_me = 29. Медианный срок обращения проданных облигаций составляет

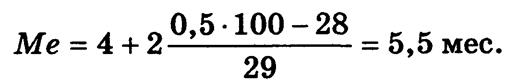
Таким образом, половина облигаций продавалась со сроком обращения менее полугода — 5,5 мес., а половина — более 5,5 мес.

В симметричных рядах распределения значения моды и

медианы совпадают со средней величиной ( = Me = Мо), а в умеренно асимметричных они соотносятся таким образом: .

В приведенном выше примере из табл. 4.1 соотношение характеристик центра распределения облигаций по сроку обращения свидетельствует об умеренной асимметрии: 3 • (5,6 - 5,5) » 5,6 - 5,4.

В анализе закономерностей распределения используются также другие порядковые характеристики: квартили и децили.

Квартили Q — это значения вариантов, которые делят упорядоченный ряд по объему на четыре равные части, а децили D — на десять равных частей. Следовательно, в ряду распределения выделяются три квартиля и девять децилей. Медиана является одновременно вторым квартилем и пятым децилем. Расчет квартилей и децилей основывается на кумулятивных частотах (частостях). Например, первый и третий квартили определяются по формулам:

первый квартиль:

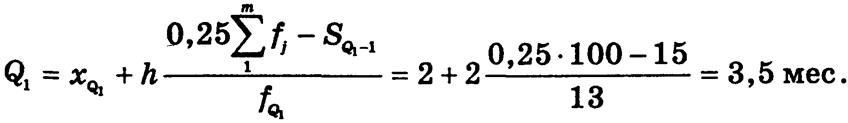
третий квартиль:

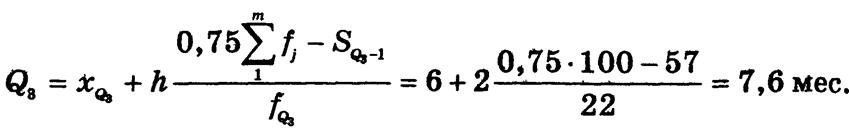
Первый и девятый децили вычисляются по формулам:

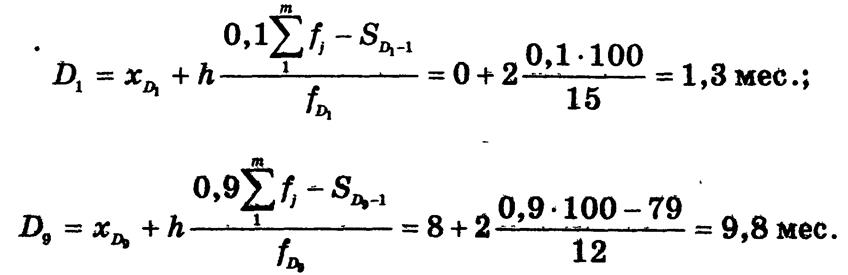
Следовательно, а ряду распределения проданных облигаций первый квартиль составляет 3,5 мес., а третий - 7,6 мес., т.е.. у 25% облигаций, проданных на вторичном рынке, срок обращения не превышает 3,5 мес., а у 75% про данных облигаций с наибольшим сроком обращения минимальный срок был 7,6 мес.

Значения децилей указывают на то, что среди 10% проданных облигаций с наименьшим сроком обращения максимальный срок составляет 1,3 мес., а среди 10% облигаций с наибольшим сроком обращения минимальный срок — 9,8 мес., т.е. в 7,5 раза больше.

Для измерения и оценки вариации используют абсолютные и относительные характеристики. К абсолютным относятся: вариационный размах, среднее линейное и среднее квадратическое отклонение, дисперсии; относительные характеристики представлены рядом коэффициентов вариации, неравномерности, локализации, концентрации.

Вариационный размах характеризует диапазон вариации, это разность между максимальным и минимальным значениями признака: R = х_max – х_min. Если крайние значения признака не типичны для совокупности, то используют квартальные или децильные размахи. Квартальный размах R_Q = Q₃ – Q₁ охватывает 50% объема совокупности, децильный  = = D₈ – D₂ — 60%, децильный  = D₉ – D₁ — 80%.