= 5 • 0,267 + 4 • 0,40 + 3 • 0,20 + 2 • 0,133 = 3,8 балла.
Осреднению подлежат не только отдельные значения вариант, но и их групповые средние хj, тогда весом будет частота (частость) каждой группы:
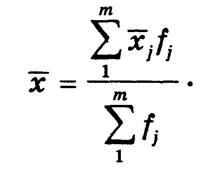
Вычисленная таким способом средняя из групповых средних называется общей.
Весом может быть также абсолютная величина, логически связанная с осредняемым показателем. Выбор весов основывается на логической формуле показателя. Поскольку средняя величина вычисляется из расчета на единицу совокупности, то вес всегда будет находиться в знаменателе логической формулы. Например, при определении средней суммы затрат на одно рекламное объявление весом будет количество рекламных объявлений. При вычислении средней суммы затрат на одного рекламодателя весом будет количество рекламодателей.
Средняя арифметическая имеет определенные математические свойства, раскрывающие ее сущность. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства лежат в основе изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на величину А или в k раз, то средняя изменится соответственно.
Например если денежные вклады граждан в Сбербанк скорректировать на уровень инфляции, составляющий 1,2, то средний размер вклада увеличится соответственно в 1,2 раза.
Средняя не изменится при пропорциональном изменении всех весов, но ее размер изменится, если произойдут структурные сдвиги.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может увеличиться за счет увеличения доли "дорогих" акций в общем количестве их продажи.
Указанные свойства средней используют в случае осреднения признаков порядковой (ранговой) шкалы. Варианты признака можно оцифровать порядковыми рангами Rj = 1, 2, ..., n или центрированными R0 = -2, -1, 0, 1, 2 (табл. 3.2). Очевидно, что R0= Rj – ½ (Rmax + Rmin). Средний центрированный балл отклоняется от среднего порядкового на величину 1/2(Rmax + Rmin).
Средний центрированный балл может принимать положительные или отрицательные значения и свидетельствует а положительной или отрицательной оценке явления. Кроме того, поскольку средний центрированный балл не зависит от размерности шкалы, его используют для сравнения оценок разных явлений.
По приведенным в табл. 3.2 данным об отношении населения к приватизации земли,
`R = 3 • 0,32 + 2 • 0,47 + 1 • 0,21 =2,11;
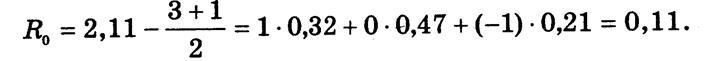
Следовательно, уровень поддержки приватизации земли положительный, но пока невысокий.
Таблица 3.2
|
Отношение к приватизации |
Доля ответов, |
Ранги |
|
|
% |
Rj |
R0 |
|
|
Полностью поддерживаю |
32 |
3 |
1 |
|
Частично поддерживаю |
47 |
2 |
0 |
|
Не поддерживаю |
21 |
1 |
-1 |
|
Итого |
100 |
x |
x |
Средняя гармоническая используется для осреднения индивидуальных значений признаков из обратных величин путем их суммирования.
Для несгруппированных данных используется средняя гармоническая простая
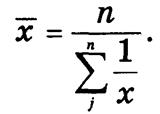
Если данные сгруппированы, то используют среднюю гармоническую взвешенную
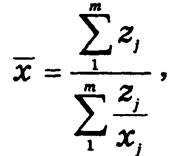
где zj — объем значении признака, т. е. zj = xjfj.
Очевидно, что среднюю гармоническую взвешенную целесообразно использовать в тех случаях, когда отсутствует информация о значении знаменателя логической формулы, т. е. отсутствуют веса.
Пример. Окупаемость затрат на развитие новаторских работ характеризуется данными табл. 3.3.
Таблица 3.3
|
Новаторские работы |
Доход от использования работ, млн ден. ед. |
Окупаемость 1 млн затрат на развитие новаторства, млн ден. ед. х |
|
Изобретения |
391 |
4,6 |
|
Рацпредложения |
377 |
6,5 |
|
Итого |
768 |
х |
Логическая формула окупаемости затрат на развитие новаторства будет иметь вид
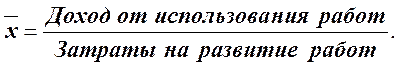
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.