Методико-практический путеводитель по темам курса "Теория статистики", страница 27

Преодолеть прерывистость такого ряда можно двумя способами:

а) скорректировав одну из частей ряда на соотношение уровней во втором периоде, например: 12 • 18/15 = 12 • 1,2 = 14,4;

б) для каждой части ряда определить базисные темпы роста, приняв уровень 2-го периода за базу сравнения, т.е.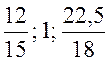

Тенденция — это основное направление развития. В рядах с четко выраженной тенденцией ее описывают аналитически с помощью определенной функции:

Y_t = f(t),

где t = 0, 1, 2, ..., n — переменная времени; Y_t — теоретические уровни ряда.

Такую функцию называют уравнением тренда. Выбор функционального вида тренда зависит от характера динамики. Так, при относительно стабильных абсолютных приростах используют линейный тренд Y_t = а + bt, при стабильных темпах прироста — экспоненту Y_t = аb^t и т. д. Соответственно параметр b в линейной функции характеризует средний абсолютный прирост, в экспоненте — средний темп роста (прироста). Параметр а в обеих функциях — это теоретическое значение уровня при t = 0.

Рассчитываются параметры трендовых уравнений методом наименьших квадратов, при этом нелинейные функции приводятся к линейному виду (например, логарифмированием lg Y_t = lg а + t lg b). Система нормальных уравнений имеет вид

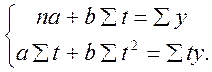
Если начало отсчета времени (t = 0) перенести в середину ряда, то St = 0, а следовательно,

где

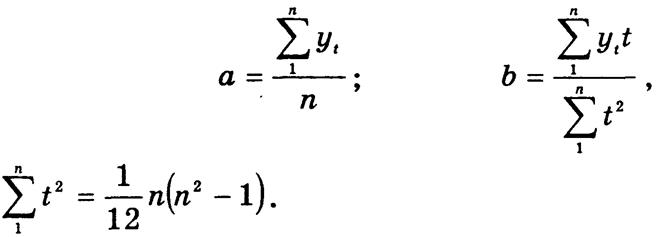
Пример. Расчет линейного тренда показан в табл. 7.3 на примере экспорта сахара. По данным таблицы n = 5; Sy_t = 219; Sty_t = 39; St² = 10.

Таблица 7.3

Год	Экспорт сахара, тыс. yt	t	tyt	Yt	yt – Yt	(yt – Yt)2
1995	37	-2	-74	36,0	-1,0	1,00
1996	39	-1	-39	39,9	-0,9	0,81
1997	43	0	0	43,8	-0,8	0,64
1998	48	1	48	47,7	0,3	0,09
1999	52	2	104	51,6	0,4	0,16
Итого	219	0	39	219	X	2,70

Параметры трендового уравнения составляют:

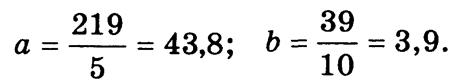
Следовательно, Y_t = 43,8 + 3,9t, т.е. средний уровень экспорта сахара составлял 43,8 тыс. т и ежегодно увеличивался в среднем на 3,9 тыс. т. При условии, что комплекс причин, формирующий тенденцию, в ближайшее время не изменится, можно продолжить тенденцию за пределы динамического ряда (экстраполировать тренд). Ожидаемый объем экспорта сахара в 2001 г. составит:

Y₂₀₀₁ = 43,8 + 3,9 × 3 = 55,5,

или

Y₂₀₀₁ = 51,6 + 3,9 × 1 = 55,5 тыс. т.

Это точечная оценка прогноза. Интервальная оценка прогноза, т.е. доверительные границы, рассчитываются с определенной вероятностью Y_t-u ± ts_p, где s_p — ошибка прогноза; t — доверительное число для принятого уровня вероятности; u — период упреждения.

Ошибка прогноза s_p рассчитывается по формуле

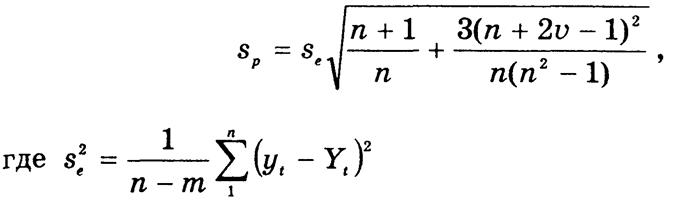
— оценка остаточной дисперсии, m — число параметров функции.

По данным табл. 7.3 s²_e = 2,70 : (5 - 2) = 0,9, а следовательно, s_e =  = 0,95.

Подкоренное выражение равно 2,1, а  = 1,45. Критическое значение двустороннего t-критерия для а = 0,05 и числа степеней свободы (n - 2) = 5 – 2 = 3 составляет t_0,95(3) = 2,57 (прил. 2).

Таким образом, ts_p = 2,57 • 0,95 • 1,45 = 3,5, а доверительные границы прогнозного уровня составляют 55,5 ± 3,5.

Если в ряду динамики тенденция четко не проявляется, то прибегают к сглаживанию ряда. Сущность его состоит в укрупнении интервалов времени и замене уровней первичного ряда средними по интервалам. Интервалы величиной т можно сформировать двумя методами:

а) последовательно, например, при т = 3 уровни объединяются: 1—3, 4—6 и т. д. Рассчитанные средние называют ступенчатыми;