Коэффициент регрессии в небольших по объему совокупностях подвержен случайным колебаниям. Поэтому необходима проверка его существенности с помощью t-критерия (Стьюдента):
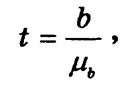
где b — коэффициент регрессии; mb — стандартная ошибка, рассчитываемая по формуле
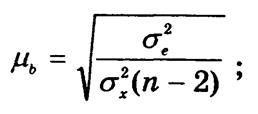
![]() — остаточная дисперсия;
— остаточная дисперсия; ![]() — дисперсия факторного признака; n —
объем совокупности.
— дисперсия факторного признака; n —
объем совокупности.
По данным табл. 6.3 ![]() = 26,75,
= 26,75, ![]() = 46,5,
n = 8, тогда
= 46,5,
n = 8, тогда
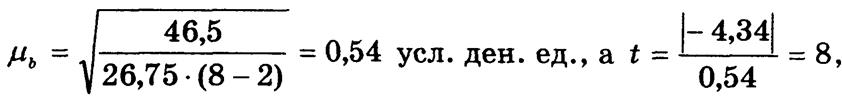
что значительно выше критического значения t0,95 (6) =2,54.
Следовательно, с вероятностью 0,95 влияние продолжительности отдыха на суточную стоимость путевок признается существенным. Для коэффициента регрессии также определяются доверительные границы b ± tmb. С вероятностью 0,95 доверительные границы коэффициента регрессии составляют
-4,34 ± 2,54 • 0,54, или -4,34 ± 1,37 усл. ден. ед.
Характеристикой относительного изменения у за счет х является коэффициент эластичности
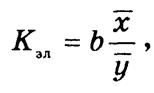
который показывает, на сколько процентов в среднем изменяется результативный признак с изменением факторного на 1%. По данным табл. 6.3
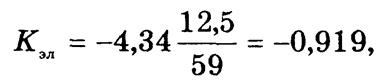
следовательно, с увеличением продолжительности отдыха на 1% суточная стоимость путевок уменьшается в среднем на 0,9%.
На основании уравнения регрессии определяются теоретические значения Y, т. е. значения результативного признака при условии, что на него влияет только фактор х, а другие факторы остаются на неизменном уровне. В приведенном примере Y — это ожидаемая стоимость путевок за счет влияния только продолжительности отдыха. Так, для х = 5 дней суточная стоимость путевки составит Y = 113,25 - 4,34 • 5 = 91,6 усл. ден. ед., что несколько отклоняется от фактического значения.
Отклонения эмпирических значений у от теоретических Y называют остаточными. Они характеризуют влияние на результативный признак всех других факторов, кроме х. Средний размер этих отклонений определяет остаточная дисперсия
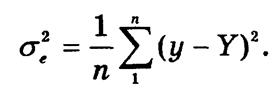
Вариацию у, обусловленную влиянием только фактора х, измеряет факторная дисперсия:
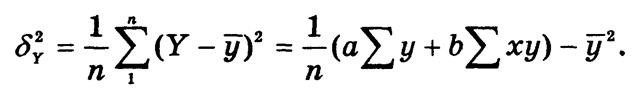
Доля факторной дисперсии в общей характеризует тесноту связи и называется коэффициентом, детерминации:
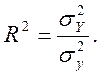
Он имеет такое же содержание, интерпретацию и цифровые границы, что и h2. По данным табл. 6.3
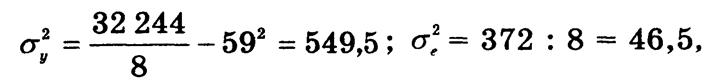
следовательно, по правилу сложения дисперсий:
![]() = 549,5 - 46,5 = 503,
= 549,5 - 46,5 = 503,
или по другой формуле
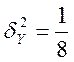 (113,25 × 472 - 4,34 × 4972) - 592 =503
(113,25 × 472 - 4,34 × 4972) - 592 =503
Тогда R2 = 503 : 549,5 = 0,915, т.е. 91,5% вариации суточной стоимости путевок линейно связаны с вариацией продолжительности отдыха, а 8,5.% вариации приходится на остальные факторы. Следовательно, связь очень тесная.
Тесноту связи можно оценить
также индексом корреляции R = ![]() , однако
интерпретируется только R2. Для линейной связи используется
линейный коэффициент корреляции (Пирсона) r:
, однако
интерпретируется только R2. Для линейной связи используется
линейный коэффициент корреляции (Пирсона) r:
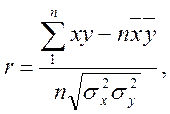
который принимает значения в пределах ±1, поэтому характеризует не только тесноту, на и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное — об обратной. В рассмотренном примере
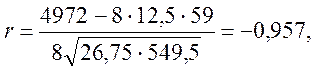
где 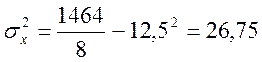 . Следовательно, связь между суточной стоимостью
туристических путевок и продолжительностью отдыха является тесной и обратной.
Абсолютное значение r равно индексу корреляции:
. Следовательно, связь между суточной стоимостью
туристических путевок и продолжительностью отдыха является тесной и обратной.
Абсолютное значение r равно индексу корреляции:
![]()
Однако для интерпретации г необходимо перейти к R2= r2.
Проверка существенности связи
осуществляется таким же образом, как и в модели аналитической группировки,
путем сравнения R2 и ![]() . Отличия касаются
только определения k1 и k2 в которых m —
число параметров уравнения регрессии. В нашем примере k1 =2 – 1 = 1,
а k2 = 8 – 2
= 6, критическое значение R20,95(1,6) = 0,500 значительно меньше фактического R2
= 0,915.
. Отличия касаются
только определения k1 и k2 в которых m —
число параметров уравнения регрессии. В нашем примере k1 =2 – 1 = 1,
а k2 = 8 – 2
= 6, критическое значение R20,95(1,6) = 0,500 значительно меньше фактического R2
= 0,915.
Пример. По данным табл. 6.4 оценим тесноту связи между уровнем эффективности экономики и надежностью делового партнерства для семи стран Восточной Европы. Поскольку информация представлена в форме интегральных показателей (оценки в баллах), необходимо провести ранжирование стран. Наименьшему значению интегрального показателя придается ранг 1, наибольшему — ранг 7. Сумма квадратов отклонений рангов составляет
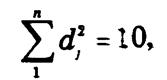
а коэффициент ранговой корреляции
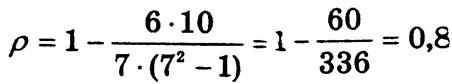
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.