Методико-практический путеводитель по темам курса "Теория статистики", страница 30

Марка бензина	Продано за период, тыс. л		Цена за 1 л в периоде, ден. ед.		Товарооборот, тыс. ден. ед.
	базисный q0	текущий q1	базисном p0	текущем p1	p0q0	p1q1	p0q1
А-76	150	95	0,46	0.48	69	45,6	43,7
А-92	120	110	0,55	0,58	66	63,8	60,5
А-95	70	125	0,60	0,66	42	82,5	75,0

Индекс товарооборота 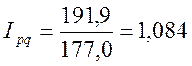 показывает, что стоимость проданного автобензина в целом по региону увеличилась на 8,4%.

Как свидетельствует индекс цен 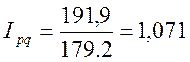, цены на бензин трех марок выросли в среднем на 7,1%.

Индекс физического объема составлял

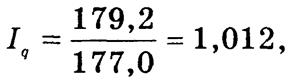
т.е. объем проданного автобензина увеличился в среднем на 1,2%.

Произведение взаимосвязанных индексов подтверждает результаты расчета: I_pq = 1,071 • 1,012 = 1,084.

Абсолютный прирост стоимости проданного автобензина в целом составляет: D_pq = 191,9 - 177,0 = 14,9 тыс. ден. ед., в том числе за счет повышения цен D_р = 191,9 - 179,2 = 12,7 тыс. ден. ед. за счет увеличения объемов продажи — D_q = 179,2 - 177,0 = 2,2 тыс. ден. ед.

Сводные индексы также могут определяться как средние из соответствующих индивидуальных индексов. Условия применения средневзвешенных индексов: однонаправленность изменений во времени и сопоставимость круга элементов.

Средневзвешенный индекс — это средний из индивидуальных индексов, взвешенных на объемы, имеющие одинаковую размерность и зафиксированные на неизменном уровне.

Такими объемами являются, в частности, Sp_iq_i, Sc_iq_i, St_iq_i. Уровень, на котором фиксируются объемы, выбирается исходя из агрегатной формулы соответствующего индекса.

Средневзвешенный индекс цен, тождественный агрегатному индексу

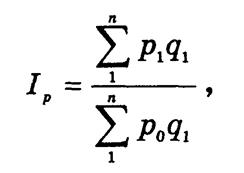
определяется по формуле средней гармонической взвешенной

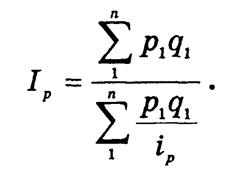
При этом условная стоимость p₀q₁ вычисляется через индивидуальный индекс цен 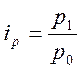, откуд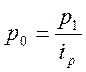а , а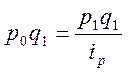

Средневзвешенный индекс физического объема вычисляют по формуле средней арифметической взвешенной

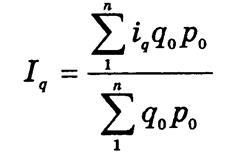
путем аналогичных преобразований условного товарооборота q₁р₀ из тождественного агрегатного индекса

 

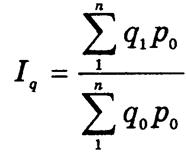
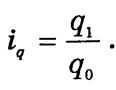через соответствующие индивидуальные индексы

Поскольку , то .

Абсолютное изменение индексируемой величины определяется по схеме, аналогичной агрегатным индексам.

Пример расчета средневзвешенных индексов цен и количества проданных акций на фондовом рынке приведен ниже.

Таблица 8.2

Рынок	Объем торгов, млн ден. ед.		Темп прироста, %		ip	iq
	Базисный период p0q0	Текущий период p1q1	цен на акции	количества акций
Первичный	80	190	+90	+35	1.9	1,35
Вторичный	40	120	+150	+20	2,5	1,20
Итого	120	310	X	X	X	X

Средневзвешенный индекс цен составляет

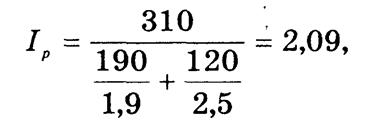
следовательно, в целом по фондовому рынку цены на акции в текущем периоде по сравнению с базисным выросли в среднем в 2,09 раза.

Средневзвешенный индекс количества проданных акций

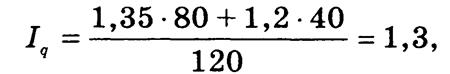
таким образом, количество проданных акций в среднем увеличилось на 30%.

Индексы средних величин характеризуют относительное изменение среднего значения показателя х.

Уровень средней зависит от значений признака х_j и соотношения весов:

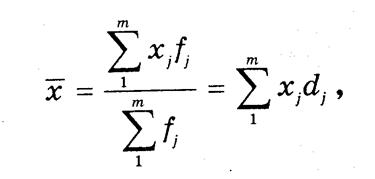
где f_j — частота; d_j — частость j-й составляющей совокупности.

Соответственно динамика средней определяется изменением значений х_j и структурными сдвигами d_j. Оценка влияния каждого из факторов осуществляется в рамках системы индексов средних величин: переменного состава, фиксированного состава и структурных сдвигов.

Индекс переменного состава  показывает изменение средней величины в целом за счет обоих факторов — признака x_j и структуры совокупности dj.

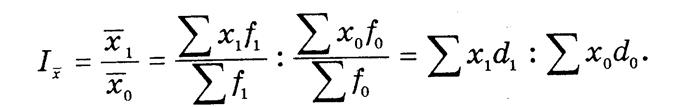
Индекс фиксированного состава I_x показывает изменение средней величины за счет изменения только значений признака при неизменной структуре совокупности:

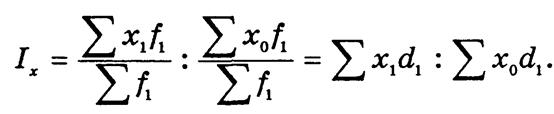
Индекс структурных сдвигов I_d показывает изменение средней за счет изменений в составе совокупности: