Методико-практический путеводитель по темам курса "Теория статистики", страница 22

Однако тесная связь может возникнуть случайно, поэтому необходимо проверить ее существенность, т. е. доказать неслучайность связи. Проверка существенности связи — это сопоставление фактического значения h² с его критическим значением  для определенного уровня существенности а и числа степеней свободы k₁ = m - 1 и k₂ = n – m, где m — число групп; n — объем совокупности. Если , то связь признается существенной. Критические значения корреляционного отношения для а = 0,05 приведены в прил. 4.

В нашем примере k₁ = 4 - 1 == 3, k₂ = 100 - 4 == 96. Из-за отсутствия в таблице критических значений k = 96 используем ближайшее (k₂ = 100), тогда

h²_0,95 (3, 100) = 0,075.

Поскольку h² 0,659 > 0,075, то связь признается существенной с вероятностью 0,95.

В модели регрессионного анализа характеристикой корреляционной связи является теоретическая линия регрессии, описываемая функцией Y = f(x), которая называется уравнением регрессии. В зависимости от характера связи используют:

линейные уравнения Y = а + bх, когда при изменении х признак у изменяется более или менее равномерно;

нелинейные уравнения, когда изменение взаимосвязанных признаков происходит неравномерно (с ускорением, замедлением или с переменным направлением связи), в частности степенное Y = ax^b, гиперболическое Y = а + b/х, параболическое Y = а + bх + сх² и т. п.

Чаще применяются линейные или приведенные к линейному виду уравнения. В линейном уравнении параметр b — коэффициент регрессии — показывает, на сколько единиц в среднем изменится у при изменении х на единицу. Он имеет единицу измерения результативного признака. При прямой связи b — величина положительная, при обратной — отрицательная. Параметр а — свободный член уравнения регрессии, т. е. это значение Y при х. == 0. Если х не принимает нулевых значений, этот параметр не имеет интерпретации. Параметры функции определяются методом наименьших квадратов, согласно которому сумма квадратов отклонений эмпирических значений у от теоретических Y минимальна: S(у - Y)² ® min. В соответствии с условием минимизации параметры вычисляются на основе системы нормальных уравнений:

Отсюда

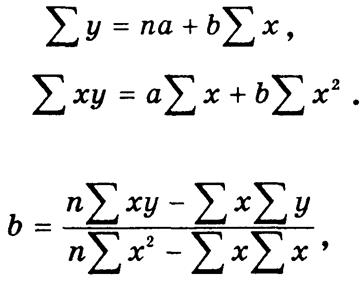
Пример. Расчет параметров линейного уравнения регрессии рассмотрим на примере связи между суточной стоимостью туристических путевок в одном из турагенств и продолжительностью отдыха (дней):

Таблица 6.3

Номер путевки	Продолжи­тельность отдыха, дней	Суточная стоимость путевки, усл. ден. ед.	ху	x2	Y	(y - Y)2	y2
	x	y
1	5	78	390	25	91,6	185,0	6084
2	14	55	770	196	52,5	6,2	3025
3	7	95	665	49	82,9	146,4	9025
4	18	30	540	324	35,1	126,0	900
5	14	53	742	196	52,5	0,2	2809
6	20	26	520	400	26,4	0,2	676
7	7	85	595	49	82,9	4,4	7225
8	15	50	750	225	48,1	3,6	2 500
Итого	100	472	4972	1464	472,0	372,0	32244

Величины, на основании которых вычисляются параметры:

Sx = 100; Sy = 472; Sxy = 4972; Sx² = 1464; n = 8;  = 100 : 8 = 12,5;  = 472 : 8 = 59. Следовательно, параметры составляют:

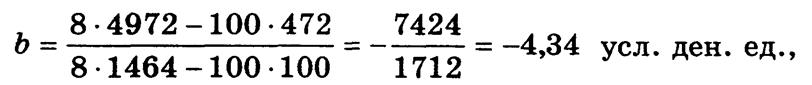
а = 59 - (-4,34) - 12,5 = 113,25.

Тогда уравнение регрессии имеет вид Y = 113,25 - 4,34x, т.е. с увеличением продолжительности отдыха на один день суточная стоимость туристической путевки дешевеет в среднем на 4,34 усл. ден. ед.