3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, а за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу. Например, при сохранении трех значащих цифр число 18598 округляют до 18600, число 152.56-до 153.
4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.
При соблюдении этих правил погрешность округления не превышает половины единицы разряда оставшейся цифры.
Погрешность округления, возникающая при округлении показаний приборов, называют погрешностью отсчитывания. Если показания прибора округляют к значению, соответствующему ближайшей отметке шкалы, то максимальная погрешность отсчитывания равна 0.5 цены деления шкалы. Если оценивать на глаз десятую или пятую долю деления шкалы, например, при определении давления с помощью микроманометра или пьезометра, то погрешность отсчитывания обычно не превышает 0.2 цены деления шкалы.
Рассмотренные выше погрешности являются максимальными. Но, так как погрешность округления внутри интервала [-ΔU,+ΔU] имеет одну и ту же вероятность, то граница доверительного интервала при доверительной вероятности α будет равна
Δх=αΔU
где ΔU - предел погрешности считывания или округления.
Точность обработки числового интервала должна быть согласована с точностью самих измерений. Вычисления, выполненные с большим числом десятичных знаков, чем необходимо, создают ложное впечатление большой точности измерений. Во всех случаях нужно придерживаться следующего простого правила: ошибка, получающаяся в результате вычислений, должна быть на порядок меньше суммарной ошибки измерений. При этом можно быть уверенным, что вычисления существенным образом не исказят результата.
Несколько слов о числе знаков при вычислении погрешностей. Как следует из материала, изложенного в разделе 5, даже при довольно большом числе измерений доверительные интервалы для σ получаются большими, т.е. величину ошибки измерения мы всегда определяем достаточно грубо. При 10 измерениях σ определяется с погрешностью более 30%. Поэтому, как правило, в этом случае для σ следует приводить одну значащую цифру, если она больше 3 , и две - если первая из них меньше 4.
Например, если S10 = 0.523, то приводим одну цифру S10 = 0.5, если S10 = 0.124, то следует дать две значащие цифры S10 = 0.12.
При n = 25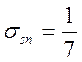 
- и,
очевидно, в этом случае нет смысла приводить для σ более двух значащих цифр,
т.е. S25 = 0.52 .
УЧЕТ СИСТЕМАТИЧЕСКОЙ И СЛУЧАЙНОЙ ПОГРЕШНОСТЕЙ.
В общем случае измерения следует организовать таким образом, чтобы погрешность результата целиком определялась систематической погрешностью измерения, которая обычно задается погрешностью измерительной аппаратуры. Для этого необходимо провести такое число измерений, чтобы случайная погрешность результата была незначительна по сравнению с систематической.
Однако на практике не всегда можно осуществить необходимое число измерений, в результате чего возникает положение, когда систематическая и случайная погрешности близки друг к другу и обе в одинаковой степени определяют точность результата измерений.
Когда мы имеем дело только с погрешностью прибора, то, указывая погрешность, определяемую его классом точности, ничего нельзя сказать о распределении погрешности внутри этого диапазона. Мы знаем только верхнюю границу возможных погрешностей.
Если к такой систематической ошибке присоединяется случайная, также ничего нельзя сказать о вероятности появления погрешностей различной величины, но можем оценить максимальное значение суммарной погрешности. Действительно, если систематическая ошибка δ, а дисперсия измерений σ2, то в качестве верхней границы суммарной погрешности при доверительной вероятности α = 0.95 можно принять
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.