Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 4

Для оценки величины случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности ее часто называют, сокращено стандартом измерений. Средней квадратичной погрешностью называется величина

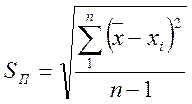
где  - среднее арифметическое значение; х_i - результаты каждого измерения;  n - число равноточных измерений.

Если число наблюдений очень велико, то подверженная случайным колебаниям величина S_П стремится к некоторому постоянному - значению

Именно этот предел и называется средней квадратичной погрешностью. Квадрат этой величины называется дисперсией измерения, это та же величина, которая входит в формулу Гаусса.

Относительная величина средней квадратичной погрешности, выраженная в процентах, называется коэффициентом вариации

%

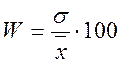Наряду с нормальным законом распределения погрешностей иногда встречаются другие типы распределения. Так, например, возможен случай, когда равновероятно появление погрешности любой величины внутри некоторого интервала, а за его пределами вероятность появления погрешности равна нулю. В дальнейшем будем рассматривать только нормальный закон  распределения погрешностей.

Если  истинное значение доверяемой величины х₀, погрешность измерения этой величины –Δx ,а среднее арифметическое -  и α вероятность того, что результат измерений х отличается от истинного значения на величину, не большую, чем Δx , то можно записать

Р (- Δх <х –  < Δх) = α

 или

Р ( - Δх < х <  + Δх) = α

Вероятность α носит название доверительной вероятности или коэффициента  надежности. Интервал значений от  + Δх до  - Δх называется доверительным интервалом.

Записанное выражение означает, что с вероятностью α результат измерений не выходит за пределы доверительного интервала от  + Δх  до  – Δх.  Разумеется, чем большей надёжности мы требуем, тем большим получается соответствующий доверительный интервал. Таким образом, мы пришли к очень важному выводу: для характеристики величины случайной погрешности необходимо задать два числа - величину самой погрешности /или доверительного интервала/ и величину доверительной вероятности. Указание только величины погрешности в значительной степени лишено смысла, так как при этом  мы не знаем, сколь надежны наши данные.

Удобство применения стандартной ошибки в качестве численного выражения погрешности наблюдений заключается в том, что этой величине соответствует определенная  доверительная  вероятность  равная  0,68 /естественно, при нормальном законе распределения погрешностей/. Для любой величины доверительного интервала по формуле Гаусса может быть рассчитана доверительная вероятность. Результаты вычислений сведены в таблицу 3.1.

Таблица 3.1

Доверительная вероятность для нормального распределения