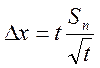
Если погрешности соизмеримы, то для доверительной вероятности α доверительный интервал равен
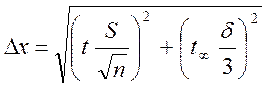
Разумеется, что если систематическая погрешность гораздо больше случайной, нет необходимости выполнять ряд измерений, достаточно выполнить его один раз. Доверительный интервал в этом случае полностью определяется систематической погрешностью прибора, т.е. его классом точности.
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
В большинстве случаев измеряется не непосредственно интересующая нас величина, а другая, зависящая от нее тем или иным образом. Например, при измерении расхода жидкости с помощью суживающегося устройства измеряется не сам расход, а перепад давлений на суживающемся устройстве, который однозначно определяет величину расхода. При таких измерениях, которые называются косвенными /в отличие от прямых, при которых определяемая величина измеряется непосредственно/, необходима также уметь вычислять погрешность измерения.
Непосредственно измеряемые величины х 1,х 2,х 3,..., х n будем считать аргументами, косвенно измеряемую – функцией
у = f (х 1,х 2,х 3,...,х n )
Среднее значение косвенно измеряемой величины находим как
где
- среднеарифметические
значения непосредственно измеряемых величин.
Вообще говоря, среднее арифметическое
значение 
можно вычислить и другим способом -
для каждого значения х i вычислить у = f (х 1,х
2,х 3,...,х n ), а затем определить из соотношения
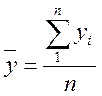
Можно показать, что если погрешности измерения малы по сравнению с измеряемой величиной, то оба способа дают достаточно близкие результаты, однако второй способ более громоздкий и, кроме того, если результаты измерений – х i распределены по нормальному закону, то закон распределения величины у в общем случае отличен от нормального. Поэтому, для определения величины среднего арифметического лучше использовать первый способ.
Учитывая, что погрешности непосредственно измеряемых величин взаимонезависимы и малы по сравнению с измеряемыми величинами, разложим функцию у = f (х i ) в ряд Тейлора. Ограничившись первым членом ряда и, используя закон слежения случайных погрешностей, можно получить выражение для определения величины доверительного интервала погрешности косвенно измеряемой величины
,
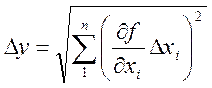где 
-
частные производные по всем к переменным при .
Подразумевается, что доверительная вероятность для доверительных интервалов погрешностей измерений одна и та же α, поэтому, доверительная вероятность доверительного интервала погрешности косвенного измерения также равна α
Граница относительной погрешности косвенного измерения
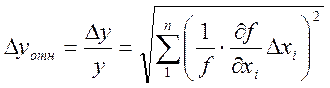
Так как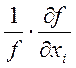
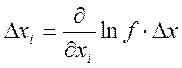, то
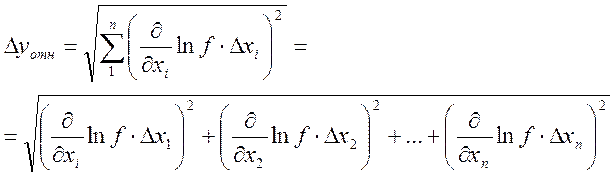
Относительная погрешность функции n переменных равна корню квадратному из суммы квадратов частных дифференциалов натуральных логарифмов функции.
На практике для нахождения относительной погрешности сначала, функцию логарифмируют, а затем находят частные дифференциалы каждой из переменных. Относительная погрешность связана простой зависимостью с величиной доверительного интервала
Рассмотрим на примере определение погрешностей косвенных измерении. Коэффициент сопротивления трения в лабораторной работе по курсу "Механика жидкости и газа" определяется как отношение перепада давления на прямом участке трубопровода Һп к перепаду давления на диафрагме Һд умноженное на постоянный коэффициент
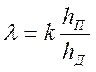
Величины Һп и Һд определяются прямыми измерениями с погрешностями ΔҺп и Δ Һд при доверительной вероятности α. Требуется найти погрешность определения коэффициента λ.
В данном случае удобнее сначала найти относительную погрешность Δλотн , для чего функцию λ логарифмируем, находим частные дифференциалы и, затем относительную погрешность
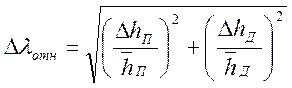
далее определяем среднее арифметическое значение
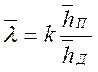
и абсолютную погрешность коэффициента сопротивления трения
Окончательный результат можно записать
ГРАФИЧЕСКОЕ ПРИБАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Результаты измерений физического эксперимента при изучении функциональной зависимости, между двумя или несколькими величинами очень часто представляются графически.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.