Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 17

С ростом числа факторов возникает необходимость в определенных приемах построения матриц. Наиболее простыми из многих возможных ме­тодов являются три приема, основанные на переходе от матриц меньшей размерности к матрицам большей размерности. Во- первых, при добавлении нового фактора   каждая комбинация уровней исходного плана  встречаемся дважды: в сочетании с верхним и нижним уровнем нового фактора. В связи с этим для построения матрицы большей размерности ис­ходный план записывают для одного уровня, а затем повторяют для другого. Второй прием основан на поэлементном перемножении вектор - столбцов матрицы. Получают вектор - столбец произведения ,  исходном  плане, а затем повторяют исходный план, а у столбца произведений меняют знаки.   Третий прием основан на правиле чередования знаков: в первом столбце зна­ки меняю поочередно,  во  втором столбце чередуют через 2, а в третьем - че­рез 4, в  - том - через .  Например, план можно построить, как показано в таблице 3.

Таблица 3. Матрица планирования.

опыта
1.	-	-	-
2.	+	-	-
3.	-	+	-
4.	+	+	-
5.	-	-	+
6.	+	-	+
7.	-	+	+
8.	+	+	+

СВОЙСТВА МАТРИЦ ПЛАНИРОВАНИЯ.

Планируемый эксперимент используется для того, чтобы получить модель, удовлетворяющую следующим требованиям: 1) точность предсказания функции отклика не должна зависеть от направления в факторном простран­стве; 2) оценки коэффициентов модели должны быть наилучшими.

Чтобы получить такую модель, матрицы планирования должны обла­дать несколькими общими свойствами:

1. Симметричность относительно центра эксперимента. Это свойство формулируется следующим образом - алгебраическая сумма элементов век­тор - столбцов каждого фактора равна нулю:

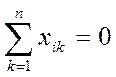
где — номер фактора,  - номер опыта, n –число опытов в матрице.

           2. Нормированость - сумма квадратов элементов каждого столбца равна числу опытов.

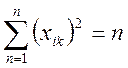
Это свойство является следствием того, что кодированные значения факторов в матрице задаются равными ± 1.

3. Ортогональность - сумма по членных произведений любых двух вектор - столбцов равна нулю:

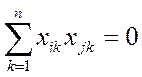               при      

4. Ротабельность матрицы - точки в матрице планирования выбраны таким образом, что точность предсказания значений функции отклика одина­кова на равных расстояниях от центра эксперимента.

Благодаря этим свойствам значительно упрощается обработка резуль­татов эксперимента методами регрессионного анализа. Так, например, для линейной модели однофакторного эксперимента (см. раздел 2) коэффициен­ты полинома определяется выражениями

                       

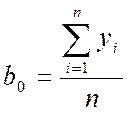
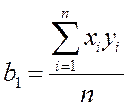
Эксперимент, проводимый по заранее составленному плану, который предусматривает искусственное изменение параметров, влияющих на про­цесс в объекте, называется активным. При пассивном эксперименте,  как пра­вило,  проводится сбор статического материала о режиме нормальной экс­плуатации объекта со случайными изменениями параметров.

Если матрица планирования активного эксперимента ортогональна, то каждый коэффициент регрессионной модели,  полученный в таком экспери­менте, оценивается независимо от остальных.  При регрессионном анализе пассивного эксперимента, когда не выполняются перечисленные свойства матрицы планирования, коэффициенты зависимы.

           Поэтому каждый член регрессионной модели, полученный при активном эксперименте, может быть отброшен без изменения остальных членов, в пассивном эксперименте от­брасывание факторов в регрессионном уравнении заставляет заново пересчи­тывать все коэффициенты уравнения.

ОСНОВНЫЕ ЭФФЕКТЫ И ЭФФЕКТЫ ВЗАИМОДЕЙСТВИЯ.