Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 21

Пусть, например, реализуется план полного трехфакторного эксперимента, матрица которого приведена в табл. 7.

Таблица 7.

Группировка систематических ошибок при нерандомизированых опытах.

опыта					опыта
1.	-	+	+		5.	-	+	-	e
2.	+	-	+		6.	+	-	-	e
3.	-	-	+		7.	-	-	-	e
4.	+	+	+		8.	+	+	-	e

В первых четырех опытах фактор  находится на верхнем уровне, а в по­следних - на нижнем. Если опыты ставились подряд в порядке номеров и внешние условия, в которых ставились первые четыре опыта, каким-то обра­зом отличались от тех, при которых проводились опыты 5 - 8, то это отличие внесет систематическую ошибку в измерение величены функции отклика. Обозначим эту ошибку через e. Предположим, что она появилась во второй серии опытов. Тогда вычисленное значение коэффициента  будет отличаться от истинного на величину.

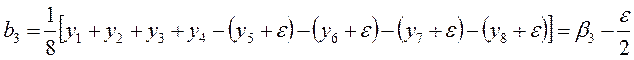
Чтобы избежать ошибки в вычислении коэффициента  опыты нужно рандомировать во времени. Если каждый опыт проводить дважды,  то, присваивая параллельным опытам номера с n+1 до 2n  (так, в факторном эксперименте  параллельные опыты будут иметь номера с 9-го по 16-й). Затем используют таблицу равномерно распределенных случайных чисел, которая приводится в любом учебнике по статистике. В случайно выбранном месте таблицы выпи­сывают числа с 1 по 16 в той последовательности, в какой они встречаются в таблице, отбрасывая числа больше 16 и уже выписанные. Пусть, например, получится такая последовательность:  7; 11; 16; 12; 13; 8; 9; 3; 10; 6; 2; 4; 14; 1; 15; 5.         Это означает, что первым нуж­но выполнить опыт № 7, вторым - № 11 (третья строка в матрице) и т.д.

Для рандомизации можно применить метод "попугая и морской свин­ки". Он заключается в том, что номера опытов записываются на карточки, которое тщательно перемешиваются и затем извлекаются.

Полученную случайную последовательность рекомендуется строго со­блюдать.

Обычная рандомизация, рассмотренная выше, во многих случаях не яв­ляется достаточно эффективным средством в борьбе с источником система­тической ошибки или источником неоднородностей в условиях проведения опытов. В принципе не исключена вероятность того, что можно получить по­следовательность проведения опытов, которая не уменьшит систематической ошибки в определении коэффициентов уравнения функции отклика. Гораздо более эффективным является планирование с ограничением на рандомиза­цию.

Ограничение на рандомизацию заключается в том, что экспериментатор, располагая определенной априорной информацией об источниках неоднородностей, четко формулирует требования к плакированию, заключаю­щееся в необходимости полностью исключить влияние источников неоднородностей.

Влияние неоднородностей можно устранить, разбивая матрицу на бло­ки таким образом, что эффект влияния внешних условий (источник неодно­родности) был смешан с определенным взаимодействием о котором известно, что оно несущественно. Если, например,  эксперимент  2³ проводят на двух   различных экспериментальных установках или в различное время суток, что вызывает различную температуру окружающей среды. И известно, что эффект тройного взаимодействия несущественный, то матрицу планиро­вания можно разбить на два блока таким образом, чтобы в одном блоке трой­ное взаимодействие было равно +1,  а в другом -1.

Опыты первого блока проводят в одно время, опыты второго - в другое. Все линейные эффекты и парные взаимодействия будут освобождены от влияния неоднородности.

Ошибка, вносимая за счет разницы температур во время проведения серии опытов, скажется на подсчете эффекта тройного взаимодействия и на подсчете свободного члена.