Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 22

                    

                   

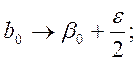
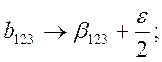
Аналогично можно разбить матрицу на 4,8 блоков и т.д.  При выборе взаимодействия, которое будет смешано с эффектом неоднородности    внешних  условий, если отсутствует достаточно надежная априорная информация, обычно выбирают или взаимодействие самого высокого порядка, или такое, которое лишено физического смысла.

Таким образом, в случае, когда экспериментатор априори ничего не знает о влиянии неуправляемых факторов, он использует обычную рандоми­зацию. Если, у него имеются сведения о наличии какого-нибудь источника неоднородности, то он использует планирование с разбиением на блоки для исключения его влияния  на эффекты исследуемых факторов.

Таблица 8.

Разбиение матрицы   два блока.

 

блока         опыта
1.                  1.	+	-	-	-	+	-	+
1.                  2.	-	-	+	+	-	-	+
1.                 3.	-	+	-	-	-	+	+
1.                 4.	+	+	+	+	+	+	+
2.                 5.	+	-	+	-	-	+	-	+e
2.                 6.	-	+	+	-	-	-	-	+e
2.                 7.	-	-	-	+	+	+	-	+e
2.                 8.	+	+	-	+	+	-	-	+1

В более сложных случаях, когда, например, два вида источников неоднородностей, можно использовать планы типа греко-латинского квадрата. Такие планы не рассматриваются в методическом пособии и приводятся в специальной литературе по планированию эксперимента в условиях неодно­родностей.

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.

Для проверки гипотез о пригодности модели для описания процесса и о значимости коэффициентов обратимся к регрессионному анализу, а именно к методу наименьших квадратов для равноточных измерений. Напомним, что при этом должны обязательно выполняться следующие положения:

1. Функция отклика есть случайная величина с нормальным законом распределения. Одной из характеристик этого распределения является дис­персия воспроизводимости, которая получается в результате усреднения дисперсии в каждой строке матрицы (построчных дисперсий), если они од­нородны. Если гипотеза об однородности дисперсии; не подтверждается, следует искать такое преобразование,  которое делает дисперсии однород­ными. Здесь довольно часто помогает логарифмическое преобразование.

2.  Ошибки в фиксировании факторов на заданных уровнях малы и ве­дут к значительно меньшим, чем ошибка воспроизводимости, изменениям величины функции отклика, т.е.

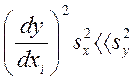
Дисперсии  каждого опыта, условия которого задаются одной строкой матрицы планирования,  (построчные дисперсии),  вычисляются по уравнению:

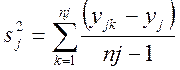
где  - число параллельных наблюдений;  - результат одного наблюдения;

 -среднее арифметическое значение результата j- го опыта, вычисля­ется из , параллельных измерений. Число степеней свобода при вычисле­нии построчных  дисперсий , так как одна степень свободы использована  для вычисления среднего арифметического. 

Стандартное отклонение одного, опыта

При расчете среднего арифметического исключить из рассмотрения грубые ошибки или промахи. Для этого можно воспользоваться методикой, изложенной в методических указаниях к методам обработки эксперимен­тальных данных.

Сравнительно простое правило обнаружения промахов основано на ис­пользовании критерия Стьюдента (1-критерия).  Измерение считается грубой ошибкой в том случае, когда табличное значение t -критерия (см. приложение 1) по модулю меньше экспериментального, рассчитанного по формуле: