3. Третий тип систематических погрешностей - погрешности, о существовании которых мы не подозреваем, хотя величина их может быть значительна. Они чаще всего проявляются при сложных измерениях. Одним из наиболее надежных способов убедиться в отсутствии таких погрешностей, провести измерение интересующей величины другим методом. Совпадение результатов служит определенной, к сожалению, не абсолютной, гарантией отсутствия такого типа систематической погрешности.
4. Следует указать еще на один источник систематической погрешности, который хотя, и не связан с измерительными операциями, может существенным образом исказить результат измерений. Речь идет о погрешностях, обусловленных свойствами измеряемого объекта.
Обнаруженная и оцененная систематическая погрешность исключается из результатов измерения, однако полностью устранить систематическую погрешность не представляется возможным, и эта остаточная погрешность будет представлять собой систематическую составляющую погрешности результата измерения.
Для того чтобы дать определение случайной погрешности, представим себе, что измерение какой-либо величины выполнено несколько раз. Если между результатами, отдельных измерений имеются различия индивидуально непредсказуемые, а присущие им закономерности проявляются лишь при большом числе опытов, то погрешность, обусловленную таким рассеиванием результатов, называют случайной погрешностью.
Говоря о свойствах погрешностей, различают грубые погрешности и промахи. Грубой погрешностью называют погрешность, существенно превышающую погрешность, определяемую свойствами аппаратуры, методом измерений и т. д. Такие погрешности могут возникнуть, например, вследствие редкого кратковременного изменения свойств объекта исследования. Грубые погрешности при статистических измерениях обнаруживают статистическими методами и исключают из рассмотрения.
Промахи - следствие неправильных действий экспериментатора. Это, например, описка при записи результатов, неправильно снятое показание прибора и т. д. Промахи обнаруживают нестатистическими методами, и их следует всегда исключать из результатов наблюдений.
Погрешности измерения делят еще на статические и динамические. Выше речь шла о статических погрешностях. Динамические погрешности - это погрешности измерений, обусловленные инерционными свойствами средств измерений. По своим свойствам динамические погрешности обычно являются систематическими погрешностями.
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Как указывалось выше, для того чтобы выяснить наличие случайной погрешности, необходимо повторить измерение несколько раз. Если каждое измерение дает несколько отличное от других измерений результат, мы имеем дело с ситуацией, когда случайная ошибка играет существенную роль.
За наиболее вероятное значение измеряемой величины следует принять ее среднеарифметическое значение, вычисленное из всего ряда измеренных значений. Это справедливо, когда выполняется нормальный закон распределения погрешностей. Однако, как показывает практика, для подавляющего большинства простых измерений он выполняется достаточно хорошо.
Нормальный закон распределения погрешностей - кривая Гаусса - может быть выведен из следующих предположений.
1. Погрешности измерений принимают непрерывный ряд значений.
2. При большом числе наблюдений погрешности одинаковой величины, но разного знака встречаются одинаково часто.
3. Часто появления погрешностей уменьшается с увеличением абсолютной величины погрешности.
Эти довольно естественные предположения приводят к закону распределения погрешностей, описываемому следующей функцией:
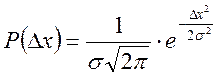
где σ² - дисперсия измерений, е - основание натуральных логарифмов. Особое значение нормального распределения определяется следующим обстоятельством в тех случаях, когда суммарная ошибка является результатом совместного действия ряда причин, каждая из которых вносит малую долю в общую погрешность, по какому бы закону ни были распределены погрешности, вызываемые каждой из причин, результат их суммарного действия приводит к гауссовскому распределению погрешностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.