Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 15

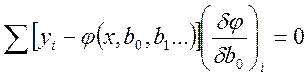
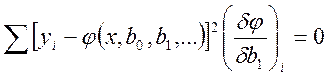
Полученная система уравнений содержит столько же неизвестных, сколько и уравнений, но в общем, виде ее решить нельзя для этого необходи­мо задаться конкретным видом функций j(х).

Как указывалось выше, при планировании эксперимента аппроксимирующая функция задается в виде полинома. Для полинома первого порядка при однофакторном эксперименте

Сумму квадратов отклонений можно представить в виде:

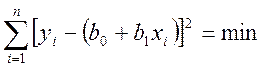
Для определения минимума:

     

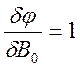
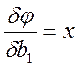
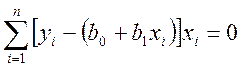
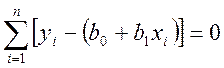
После решения системы линейных алгебраических уравнений

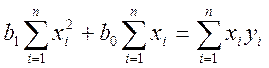
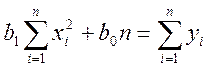
определим коэффициенты:

        

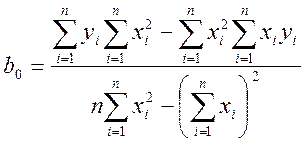
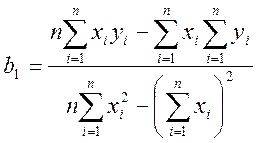
Для однофакторного эксперимента и полинома, второго порядка имеем:   

           

                          

                    

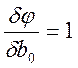
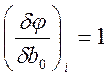
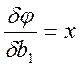
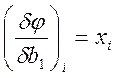
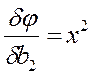
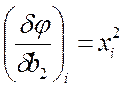
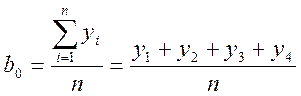
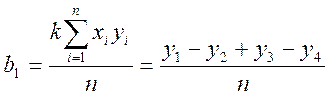
Система линейных алгебраических уравнений имеет вид:

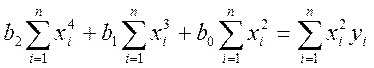
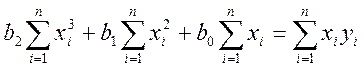
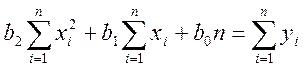
Коэффициенты   могут быть найдены с помощью метода определителей

                 

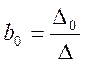
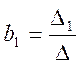
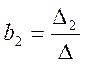
где  - главный определитель системы; - определители, получаю­щиеся заменой в главном определителе столбца коэффициентов  при    соответственно столбцов свободных членов.

МНК как вычислительный прием требует значительных вычислитель­ных затрат, связанных с определением сумм при коэффициентах        в

системе нормальных уравнений (1),(2). Эти вычисления удобно проводить с помощью программируемого микрокалькулятора "Электроника БЗ-21", по­зволяющего получить коэффициенты  и    непосредственно после вы­полнения программы для линейного уравнения регрессии, а для квадратич­ной аппроксимации - автоматизировать подсчет сумм в системе уравнений (2).

Программа  линейной  аппроксимации  и  программа  подсчета  сумм  в  системе   уравнений  (2) приведены в  приложениях 12, 13.

ВЫБОР ФАКТОРОВ. АНАЛИЗ АПРИОРНОЙ ИНФОРМАЦИИ ПРИ ВЫБОРЕ ЭКСПЕРИМЕНТАЛЬНОЙ ОБЛАСТИ ФАКТОРНОГО ПРОСТРАНСТВА.

Весь процесс планирования экспериментов можно разбить на не­сколько этапов, часть из которых полностью формализована, а часть основа­на на эмпирико-интуитивном подходе. Построению плана эксперимента

предшествует важный этап принятия именно интуитивных решений по вы­бору факторов и области экспериментирования.

1. В рассмотрение следует включить все факторы, которые могут суще­ственно влиять на процесс.

2. Выбранные факторы должны быть доступны измерению с точностью примерно на порядок большей, чем измерение выходной величины. Кроме того, факторы должны быть независимыми величинами.

3. При оценке границы области определения факторов должны учиты­ваться ограничения трех типов: а) физические, например, ограничения по температуре, давлению, скорости передачи сигналов; б) технико-экономические, связанные, например, со стоимостью аппаратуры; в) технологические,  связанные с особенностями применённых в объекте ис­следования конструкционных материалов.

4. Обычно процесс исследования начинается в условиях, когда имеются некоторые сведения об объекте. Все сведения об объекте,  полученные в ре­зультате предыдущих исследований, из литературы, на основании аналогий со сходными объектами или из теоретических соображений, называют апри­орной информацией. Именно из априорной информации получают представ­ление о функции отклика и факторах, о кривизне поверхности отклика и т.д.

5. Анализ априорной информации часто позволяет определить такие значения факторов, при которых получаются результаты близкие к опти­мальным. Эту точку рассматривают как нулевой (основной уровень). По­строение плана эксперимента сводится к выбору точек симметричных относительно нулевого уровня.

Выбранный нулевой уровень должен удовлетворять следующим требо­ваниям: 1) значения функции отклика в этой точке должно быть наилучшим из всех известных; 2) координаты нулевого уровня должны лежать внутри об­ласти определения.

6. Следующий этап - это выбор интервалов варьирования факторов. Пусть факторы в эксперименте варьируются на двух уровнях, симметричных относительно нулевого. Верхний уровень фактора можно получить прибав­лением определенного числа к основному уровню, а нижний - вычитанием этого же числа от нулевого уровня. Это число называют интервалом варьи­рования фактора. Таким образом, задача выбора уровней сводится к более простой задаче выбора интервалов варьирования. Обычно для упрощения записи условий эксперимента и обработки результатов масштабы по осям выбирают так, чтобы нижний уровень соответствовал -1, верхний +1, а основной - О.