Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 27

Координаты уравнения регрессии рассчитывают по приведенным выше формулам и снова проверяют гипотезу об адекватности.

В случае планирования двухфакторного эксперимента для отыскания зависимости в виде полинома второго порядка:

последовательность решения задачи следующая.

Проводится первая серия опытов (выполняются четыре опыта) и про­веряется адекватность линейного уравнения регрессии:

Если адекватность линейной модели не подтверждается, ставят вторую серию опытов для получения уравнения регрессии второго порядка. Планы экспериментов для второй серии опытов могут быть различными (см. рис.3)

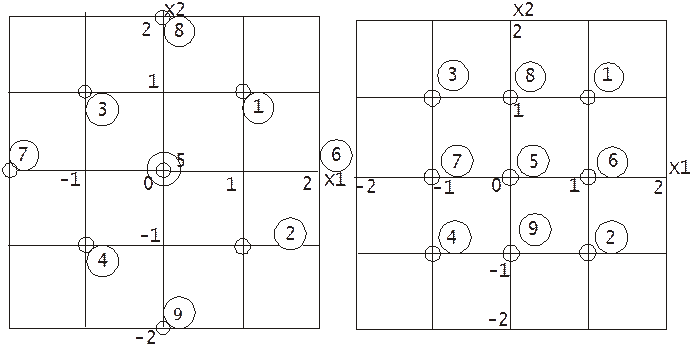Рис. 3. Расположение опытных точек при второй серии опытов.

Первый план применяют в тех случаях, когда погрешность описания функ­ции отклика во всей области изменения факторов должна быть приблизительно одинакова.  Второй план - если требуется более точно описать цен­тральную область исследования. Коэффициенты уравнения регрессии опре­деляются с помощью таблиц, приведенных в приложении. Там же приведены матрицы планирования трехфакторного эксперимента и таблицы для расчета коэффициентов уравнения регрессии.

ЗАКЛЮЧЕНИЕ

Изложенные в методическом пособии основные приемы вычисления погрешностей измерения при обработке результатов экспериментальных данных, не охватывают всех случаев, встречающихся на практике.

Основное внимание уделено случаю нормального распределения погрешности как наиболее часто встречающемуся на практике. Освоение примененных при этом способов, может оказаться полезным не только при обработке данных лабораторных работ, но и при выполнении студенческих научно-исследовательских работ.

Обработка экспериментальных данных может быть значительно облегчена применением вычислительной техники.

ЛИТЕРАТУРА

1 Зайдель А.И. Экспериментальные оценки ошибок измерений. Л., "Наука",1967, 89с.

2. Чепуренко В.Г., Нижних В.Г., Сололова А.И. Вычисление погрешностей измерения. Киев, "Вища школа", 1978, 37 с.

ПРИЛОЖЕНИЕ 1

(обоснование полного расширения)

;;

;  

;       ;

;

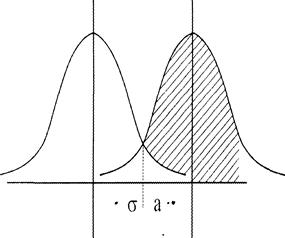
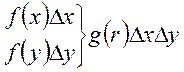
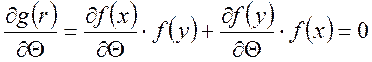
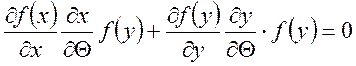
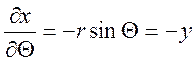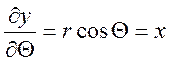
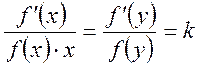
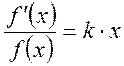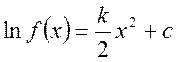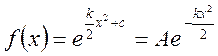
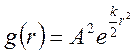
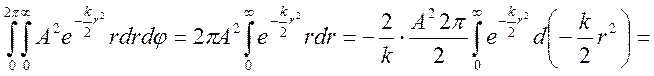
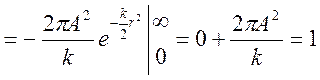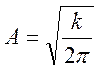
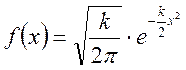
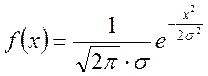
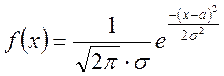
ПРИЛОЖЕНИЕ 2.

Значение t-критерия Стьюдента и критерия  для уровня значимости 0,05.

Число степеней свободы         f.	t		Число степеней свободы          f.	t
1.	2,71	0,0039	11.	2,2	4,6
2.	4,3	0,103	12.	2,18	5,2
3.	3,18	0,352	13.	2,16	5,9
4.	2,78	0,71	14.	2,14	6,6
5.	2,57	1,14	15.	2,13	7,3
6.	2,45	1,63	16.	2,12	8,0
7.	2,36	2,17	17.	2,11	8,7
8.	2,31	2,73	18.	2,10	9,4
9.	2,26	3,32	19.	2,09	10,1
10.	2,23	3,94	20.	2,09	10,9

ПРИЛОЖЕНИЕ 3.

Значение критерия Фишера для уровня значимости 0,05.