Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 13

В настоящее время показано, что наибольший эффект математическая стати­стика может принести тогда, когда ее аппарат используется на самом первом этапе при планировании эксперимента. Планирование эксперимента позволяет  

- уменьшить ошибку эксперимента;

- сократить количество опытов;

- получить математические модели, обладающие некоторыми оптимальными свойствами;

-принимать решения на основе четких формализованных правил.

 Разумеется, методы математического планирования не освобождают иссле­дователя от принятия ряда неформализованных решений, к которым относят­ся выбор модели процесса, выбор определяющих факторов и интервалов их варьирования и т. д. То есть математическое планирование является ценным рабочим инструментом в руках квалифицированного специалиста. С целью повышения качества подготовки специалистов введен в учебный план курс "Основы научных исследований", одним из разделов которого является планирование эксперимента. Предлагаемое методическое пособие ставит своей задачей ознакомить студентов с основами математического планирования эксперимента с тем, чтобы при выполнении лабораторных работ, исследовательских курсовых и дипломных проектов научно-исследовательской работы будущие специалисты могли четко поставить за­дачу исследования, выбрать - способ и стратегию ее реализации, провести анализ и интерпретацию результатов. Методические указания составлены с учетом того, что кафедра  “ Гидравлических машин'' обучает иностранных сту­дентов.

Основные определения, принятые при планировании эксперимента, рассмот­рим на примере исследования "черного ящика", в качестве которого возьмем объект (рис. I), который описывается, с одной стороны, перечнем способов воздействия на него/  …_, а с другой - набором измеримых характеристик /выходов/ у₁, y_2,….  Если и объектом исследования является гидравлическое или пневматическое устройство, то входными величинами могут быть давление, расход жидкости, сопротивление дросселя и т. д.

Переменные , принято называть факторами. Выходными величинами могут быть - перемещение, частота вращения, усилие, быстродействие и коэффициент по­лезного действия и др.

В зависимости от условия решаемой при планировании эксперимента задачи выходная величина  называется откликом, функцией отклика, функцией цели, параметром оптимизации.

Обычно аналитическая связь между функцией отклика и факторами неизвестна, а известны сами факты , и подлежащие исследованию выход­ные величины .

Пусть выходная величина является неизвестной функцией  факторов .

В таком случае можно выделить три типичные задачи планирования эксперимента:

1.Раскрытие механизма явления, т.е. нахождение такого аналити­ческого выражения,

которое в области возможных значений факторов , достаточно точно совпадает с неизвестной зависимостью j(Х). Область возможных или допустимых значений факторов , называется областью определения.

В методе Бокса-Уилсона функцию отклика аппроксимируют степенным рядом

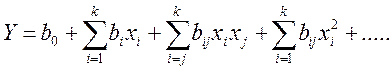
Коэффициенты полинома … рассчитывают по результатам экспе­римента. Эксперименты по раскрытию механизма явления называют интерполяционными  или  регрессионными.

2.Определение экстремума /максимума или минимума/ функции откли­ка в области ее определения. Такие эксперименты называют экстремальными.

3. Выбор подходящей модели для описания объекта или определение параметров известной функциональной зависимости.

В методическом пособии рассмотрена первая задача-планирование эксперимента при раскрытии механизма явления.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Как следует из вышесказанного, интерполяционная задача сводится к определению коэффициентов полинома (I) по результатам экспериментов.  Известно, что через любые п точек с координатами  всегда можно про­нести кривую, выражаемую аналитически полиномом (п-1) степени, так, что она в точности пройдет через каждую точку  (рис. 2) Однако такое решение вопроса не является удовлетворительным; как правило, нерегулярное поведете экспериментальных точек связано не с объективным характером зависимости У от X, а исключительно с ошибками измерения. Желательно обработать