Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 23

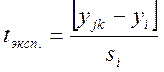
Рассмотрим пример применения этого правила. Предположим, что в четырех повторных опытах получены следующие результаты:

0.024; 0,028; 0,028; 0,034.  Поскольку результаты четвертого опыта несколько отличаются от остальных, проведем проверку, не является ли этот опыт гру­бым измерением. По первым трем опытам проводится вычисление среднего арифметического.

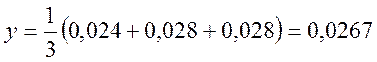
Определяется ошибка опыта

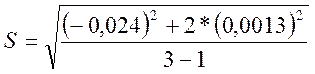
Экспериментальное значение t-критерия равно

Табличное значение критерия Стьюдента при числе степеней свободы f = 2 и уровне значимости 0,05 равно 4,3. Экспериментальное значение мень­ше табличного, поэтому с вероятностью 95% можно утверждать, что между результатами нет существенной разницы, и четвертый опыт не является про­махом. Следовательно, значение среднего арифметического следует вычислять по результатам четырех опытов и оно ровно 0,0295.

Дисперсия всего эксперимента в целом получается за счет объединения построчных дисперсий.

Эта величина называется дисперсией функции отклика или дисперсией

воспроизводимости и обозначается . Прежде чем рассчитать дисперсию воспроизводимости, необходимо проверить гипотезу об однородности построчных дисперсий,  т.е. об отсутст­вии среди всех суммируемых дисперсий величин, значительно превышаю­щих все остальные.

Проверка однородности дисперсий проводится с помощью различных статистических критериев. Наиболее употребляемым является критерий Фи­шера и Кохрена.

Критерии Фишера  предназначен для сравнения двух дисперсий и пред­ставляет собой отношение большей дисперсии к меньшей. Рассчитанная ве­личина сравнивается с табличным значением F-критерия (см. приложение 2). Если полученное отношение дисперсий меньше табличного (для соот­ветствующих степеней свобода и выбранного уровня значимости), то диспер­сии незначимо отличаются друг  от друга, т. е. они однородны.

Пусть в одном опыте,  результат которого является средним из четырех

наблюдений,   а в другом,  усредненном по трем параллельным на­блюдениям, . Для проверки гипотезы об однородности дисперсий вычисляют дисперсионное отношение.

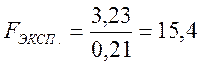
Табличное значение F -критерия  (для числа степеней свободы числителя 

и знаменателя )  равно 19,2. Поскольку экспериментальное значе­ние F -критерия меньше табличного, то с вероятностью 95% можно утвер­ждать, что гипотеза об однородности дисперсии выполняется.

Если сравниваемое количество дисперсий больше двух и число наблю­дений во всех опытах одинаково, то для проверки гипотезы об однородности дисперсий пользуемся критерием Кохрена (G -критерием),  равным отноше­нию максимальной дисперсии к сумме всех дисперсий.

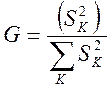
Гипотеза об однородности дисперсий подтверждается, если экспери­ментальное значение критерия Кохрена не превышает табличного (см. при­ложение 3).

При неравном числе параллельных опытов используют приближенный критерий Бартлетта (В - критерий).  Для этого вычисляют средневзвешен­ную дисперсию.

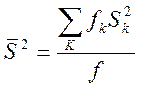
где  - суммарное число степеней свободы .

Экспериментальное значение критерия Бартлетта равно:

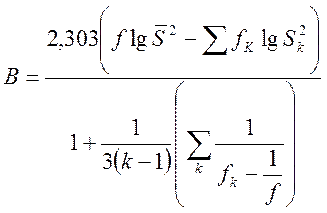
Табличное значение B - критерия приближенно равно - критерию с

k-1 степенями свободы,  если . Значения  - распределения приве­дено в приложении 1.

Если найденная величина B превосходит значение  при выбран­ном уровне значимости, то  гипотеза об однородности не подтверждается.

Ещё раз подчеркнем, что только после принятия гипотезы об однород­ности дисперсии можно приступать к вычислению дисперсий  воспроизводи­мости в целом.

При одинаковом числе параллельных опытов дисперсия  воспроизводи­мости и эксперимента вычисляется по формуле:

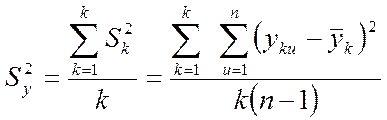
Если число параллельных опытов в каждой строке матрицы неодинаково, то дисперсия эксперимента рассчитывается по формуле:

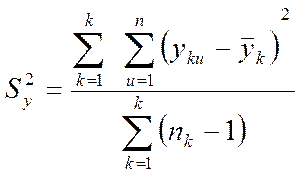
|где  - число параллельных измерений в  К - ой строке.

ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ.

Одним из наиболее важных вопросов в планировании эксперимента яв­ляется вопрос о пригодности полученной модели для описания поверхности отклика, в которой проводился эксперимент. Проверка пригодности модели называется проверкой ее адекватности.