Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 7

Сравнивая приведенные в таблице данные с данными таблицы 3.1, легко убедиться, что при больших n величинах  t стремятся к ε.  Это естественно, т. к. с увеличением n, S_П стремится к σ.

Рассмотрим несколько примеров использования коэффициентов Стьюдента. Пусть среднее арифметическое из пяти измерений равно 31   ,2. Средняя квадратичная погрешность, определенная по пяти этим измерениям равна 0,24.  Необходимо найти доверительную вероятность того, что среднее арифметическое отличается от истинного значения не более чем на 0.2, т.е. будет выполняться неравенство.

31.0 < х < 31.4

Значение коэффициента Стьюдента найдем, поставив наши величины

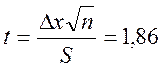
По таблице 5.1 находим при n = 5; t = 1.5; α = 0.8, а при α = 0.9  t=2,1. Обычно можно удовлетвориться ответом, что доверительная искомая вероятность лежит между 0.8 и 0.9. Если нужно получить более точное значение, можно прибегнуть к линейной интерполяции результатов.

В заключение этого раздела кратко рассмотрим вопрос определения погрешности.  Если мы определяем S_П из очень большого числа измерений, то полученная величина мало отличается от своего предельного значения σ. Но, когда n не велико, то S_П отягчено, случайными погрешностями, очевидно, тем меньшими, чем больше n. Точно так же, как и для результатов измерений, существует закон распределения, дающий возможность установить доверительную вероятность того, что определенная из n измерений погрешность будет отличаться от σ в некоторое заданное число раз.

Для определения доверительного интервала, внутри которого находится σ,  можно воспользоваться  приближенной формулой

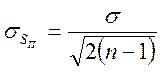
Здесь - средняя квадратичная погрешность величины, когда она вычислена из n измерений. Это выражение справедливо для n > 80, но в случае грубых оценок его можно использовать и при меньших n.

Лекция 2.

НЕОБХОДИМОЕ ЧИСЛО ИЗМЕРЕНИЙ.

Для уменьшения случайной ошибки результата измерения, как установлено выше, могут быть использованы два пути: улучшение точности измерения, и увеличение числа измерений, т.е. использование соотношения

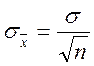
В этом разделе будем говорить только о последнем приеме, считая, что все возможности усовершенствовать технику эксперимента уже использованы. Пусть систематическая ошибка, определяемая классом точности прибора, равна δ.

Известно, что уменьшать случайную ошибку целесообразно только до тех пор, пока общая погрешность измерений не будет полностью определяться систематической ошибкой. Для этого необходимо, чтобы доверительный интервал, определенный с выбранной степенью надежности, был существенно меньше величины систематической ошибки. Строгую количественную оценку - на сколько меньше сделать трудно, однако можно исходить из того что, как правило, нет необходимости определять общую ошибку с точностью большей 10%. Это означает, что должно быть выполнено условие   .          Практически нужно удовлетвориться гораздо менее жестким требованием или даже.

Это следует из правила учета случайной и систематической погрешности, которое будет рассмотрено ниже.

Надежность α, с какой мы хотим установить доверительный интервал, в большинстве случаев, встречающихся при технических измерениях, не превышает 0,95. Для оценки необходимого числа измерений можно воспользоваться таблицей 6.1.

Таблица 6.1

	0.5	0.7	0.9	0.95	0.99	0.994
1.0	2	3	5	7	11	17
0.5	3	6	13	18	31	50
0.4	4	8	19	27	46	74
0.3	6	13	32	46	78	130
0.2	13	29	70	100	170	280
0.1	47	110	270	390	700	1100
0.05	180	430	1100	1500	2700	4300
0.01	4500	11000	27000	38000	66000	110000