Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 24

Рассеяние экспериментальных точек относительно найденного уравне­ния регрессии характеризуется остаточной дисперсией или дисперсией адек­ватности .

Дисперсия адекватности равна сумме квадратов отклонений, от­несенной к одной степени свободы.

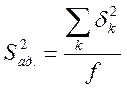
Здесь число степеней свободы - разность между числом опытов и чис­лом коэффициентов модели, которые вычислены по результатам этих опытов независимо друг от друга, т.е.

 где (n+1) - число коэффициентов модели.

Для проверки гипотезы об адекватности модели наиболее часто ис­пользуют критерий Фишера, который сравнивают с экспериментальным отношением.

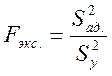
Если экспериментальное значение не превышает табличного значе­ния F -критерия, то с соответствующей доверительной вероятностью мо­дель можно считать адекватной. При превышении табличного значения ги­потеза об адекватности отвергается.

Рассмотрим пример проверки адекватности линейной модели, полу­ченной по результатам полного факторного эксперимента. Матрица планиро­вания и результаты опытов приведены в таблице 9.

 Таблица 9 Матрица планирования и результаты эксперимента.

опыта.						опыта.
1.	-	+	-	4,2	3,9	5.	-	+	+	4,7	5,35
2.	+	-	-	1,3	2,15	6	+	+	+	6,8	6,5
3.	-	-	-	1,5	1,0	7	-	-	+	2,4	2,45
4.	+	+	-	5,2	5,05	8	+	-	+	4,0	3,60

Получены следующие значения коэффициентов регрессии:

                             

                

                  

По результатам эксперимента вычислена дисперсия воспроизводимости   .

Уравнение линейной модели имеет вид:

Расчетные значения функции отклика приведены в матрице планиро­вания. Определим дисперсию адекватности:

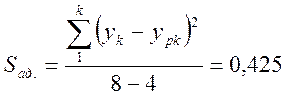
Значения критерия Фишера:

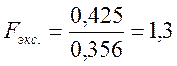
Так как, то линейная модель адекватна и эффектами взаимодействия можно пренебречь.

Благодаря кодированию факторов и ортонормированности матрицы плани­рования дисперсия и доверительные интервалы коэффициентов для всех коэффициентов регрессии получаются одинаковыми:

                       

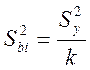
где  - табличное значение критерия Стьюдента для уровня значимости   ,

взятого при числе степеней свободы , при котором определяли . Зна­чение 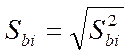  называют стандартным отклонением коэффициента  регрессии.

Коэффициент значим, если его абсолютная величина больше довери­тельного интервала. Чем уже доверительный интервал, тем с большей уве­ренностью можно говорить о значимости коэффициента.

Проверим значимость коэффициентов в приведенном выше примере.

       

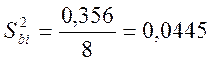
Табличное значение t- критерия для восьми степеней свобода при 5% уровне значимости равно 2,31, отсюда   =±2,31*0,218 =±0,49

Поскольку коэффициенты линейных эффектов по абсолютной величи­не больше, а эффект взаимодействия меньше, чем доверительный интервал, то можно принять гипотезу о не значимости коэффициентов взаимодействия.

Лекция 7.

ИНТЕРПРЕТАЦИЯ МОДЕЛИ.

После построения математической модели наступает новый этап не­формализованных решений, этап интерпретации полученных результатов, т.е. объяснения и анализа результатов эксперимента. Вначале оценивают, как влияют факторы на величину функции отклика. Количественной мерой этого влияния является абсолютная величина коэффициента регрессии. О направ­лении влияния факторов говорят знаки коэффициентов. Если коэффициент положителен, то с увеличением фактора значение функции отклика растет, и наоборот, если коэффициент отрицателен, то рост этого фактора приводит к уменьшению величины функции отклика. Если ведется поиск максимума в области изменения факторов, то благоприятно увеличение тех факторов, ко­эффициенты которых положительны и уменьшение тех, коэффициенты кото­рых отрицательны. Естественно, что при поиске минимума функции отклика рекомендации противоположны.