Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 26

Рассмотрим пример планирования однофакторного эксперимента. Предположим, исследуется характеристика центробежного насоса, которая в общем случае графически может быть изображена несимметричной пара­болой. Можно сразу планировать эксперимент, ориентируясь на многочлен третьего порядка, однако более рационально на первом этапе попытаться провести аппроксимацию линейным уравнением.

Выбрав шаг,   изменения переменной и произведя кодирование фактора.  Проводим первую серию опытов согласно матрице планирования, приве­денной в таблице 10.

Таблица 10.  Первая серия опытов.

опыта
1.	0	-1	15	16,72
2.	100	0	16,5	13,07
3.	200	1	7,7	9,42

Методом наименьших квадратов определяем коэффициенты  и  линейного уравнения регрессии:

Определение коэффициентов уравнения регрессии может быть облегчено применением таблиц, приведенных в приложении. Общей  формулой для вычисления любого коэффициента регрессии по таблицам 4 + 6,8,9,11 служит выражение:

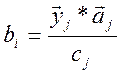
где  - вектор-столбец результатов изменения;

 - вектор- столбец для  соответствующего коэффициента ;

 -множитель коэффициента  приводимый, в той же таблице.

Для линейного уравнения.

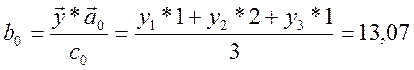
Далее определяем адекватность уравнения. Для этого находим дисперсию адекватности:

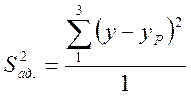
В данном случае число степеней свободы  =1,  так как по трем опытам най­дены два независимых коэффициента уравнения    и  .

Зная погрешность, с которой проводился эксперимент,  рассчитываем критерий Фишера:

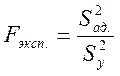
и сравниваем его с табличным значением для соответствующей довери­тельной вероятности. Если  то линейную модель можно счи­тать адекватной и опытов больше не проводить. Если же   гипо­теза адекватности линейной модели отвергается и проводится новая серия опытов с целью определения коэффициентов уравнения регрессии второго порядка.

Интервал варьирования фактора уменьшается вдвое и производится новое кодирование:

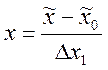
Составляется новая матрица планирования (табл.11).

Таблица 11. Вторая серия опытов.

опыта
1.	0	-2	15	14,96
2.	100	0	16,5	16,25
3.	200	2	7,7	7,66
4.	50	-1	15,6	16,06
5.	150	1	13,8	13,96

Отметим, что для ее заполнения нужно провести всего два опыта, опы­ты 4 и 5, остальные опыты уже проведены.

По результатам опытов определяются коэффициенты квадратичной аппроксимации,  и проверяется ее адекватность.

В случае если квадратичная аппроксимация описывает процесс неаде­кватно, переходят к поиску коэффициентов уравнения регрессия третьего порядка.

Эти коэффициенты можно найти по результатам уже проведенных пяти опытов (ищется четыре коэффициента уравнения регрессии и остается одна степень свободы для определения дисперсии адекватности):

                 

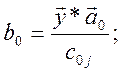
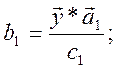
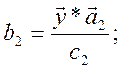
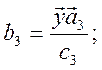
Если гипотеза об адекватности полученного уравнения снова отвергнута, ставят третью серию из четырех опытов.

Таблица 12. Третья серия опытов.

опыта
1.	0	-4	15	14.96
6.	25	-3	15.6	15.52
4.	50	-2	15.9	16.03
7.	75	-1	16.1	16.33
2.	100	0	16.5	16.22
8.	125	1	15.7	15.48
5.	150	2	13.8	13.83
9.	175	3	11.1	11.35
3.	200	2	7.7	7.75