Приведем примеры пользования таблицей. Предположим, что измеряется скорость потока с помощью термоанемометра, имеющего погрешность 2 м/с, средняя квадратичная погрешность единичного измерения также равна 2 м/с. Сколько измерений нужно сделать, чтобы получить ошибку не более 3 м/с с надежностью 0,95?
Предположим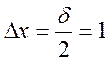 
м/с , S
= 2м/с доверительный интервал в долях S равен 0,5. Из таблицы 6.1 для α =0.95 и
ε =0.5 находим необходимое число опытов 18.
Решим ту же задачу при средней квадратичной погрешности равной 10 м/с. В этом случае для α=0.95 и 8=0.1 число опытов получается равным 390. Из приведенных примерок видно, что в первом случае мы получили реальное число опытов, во втором - практически выполнить такое число измерений достаточно трудно. Это позволяет сделать заключение, что увеличением числа измерений можно устранить влияние случайной ошибки на результат измерения, если средняя квадратичная погрешность не более чем в 4 - 5 раз превышает систематическую ошибку.
При больших значениях для существенного уменьшения случайной погрешности требуется выполнить сотни и тысячи измерений, что часто бывает практически невыполнимо. В таких случаях для уменьшения погрешности результата нужно менять методику измерений с тем, чтобы уменьшить величину случайной погрешности.
ОБНАРУЖЕНИЕ ГРУБЫХ ПОГРЕШНОСТЕЙ.
Если в полученной группе результатов наблюдений имеются несколько резко отличающихся от остальных, а наличие ошибки или описки в снятии показаний не установлено, следует проверить, не являются ли они грубыми погрешностями, подлежащими исключению. Задача решается статистическими методами, основанными на том, что распределение, к которому относится рассматриваемая группа наблюдений, можно считать нормальным.
Для этого случая Ф. Ё. Граббс рассчитал границы допустимых максимальных и минимальных значений при n наблюдений. В дальнейшем были табулированы q - процентные точки распределения максимальных по модулю отклонений результатов наблюдений от их среднего значения
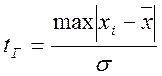
Это распределение удобнее для расчетов и приведено в таблице 7.1. Чтобы проверить возможность отбросить наблюдение хВ нужно вычислить
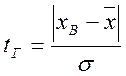
где 
и σ вычисляются
с учетом всех n результатов наблюдений. Затем, выбрав уровень значимости q /при
технических измерениях обычно 1÷5%/, нужно по таблице 7.1. найти значение tГТ,
отвечающее этому уровню и числу наблюдений. Если tГ > tГТ,
то хВ можно отбросить, так как вероятность появления наблюдения,
дающего tГ > tГТ мала и равна принятому уровню значимости.
С уменьшением q растет tГТ и условие отбрасывания эксперимента
выполняемся труднее
ПОГРЕШНОСТЬ ОКРУГЛЕНИЯ, ОТСЧИТЫВАНИЯ, ТОЧНОСТЬ ВЫЧИСЛЕНИЙ.
Числовое значение результата измерения должно быть представлено так, чтобы оно оканчивалось десятичным знаком того же разряда, что и значение его погрешности? Большее число разрядов не имеет смысла, так как не уменьшит неопределенности результата, характеризуемой погрешностью. Меньшее число знаков, которое можно получить округлением числа, заграбило бы результат.
Округления при обработке результатов наблюдений следует выполнить, руководствуясь следующими правилами:
1. Округлять результат измерения следует так, чтобы он оканчивался цифрой того же разряда, что и значение его погрешности. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду числового значения погрешности.
2. Если цифра старшего из отбрасываемых разрядов меньше 5, то оставшиеся цифры числа не изменяют. Лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают.
Например, числовое значение результата измерения 85.6342 при погрешности ± 0.04 следует округлить до 85.63. То же число при погрешности ± 0. 012 следует округлить до 85.634. Число 165245 при сохранении четырех значащих цифр должно быть округлено до 165200, а число 165.245 - до 165.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.