Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 6

Средняя квадратичная погрешность среднего арифметического равна средней квадратичной погрешности отдельного результата, деленной на корень квадратный из числа измерений. Из этого следует, что, желая повысить точность измерения в два раза, нужно вместо одного выполнить четыре измерения, а увеличение числа измерений в 100 раз приведет к десятикратному увеличению точности. Естественно, что все выше сказанное относится к измерениям, при которых точность результата определяется только случайной ошибкой.

При практической работе очень важно строго разграничивать применение средней квадратичной погрешности отдельного измерения и средней квадратичной погрешности среднего арифметического . Последняя применяется, если необходимо оценить погрешность того числа, которое получено в результате всех измерений. В тех случаях, когда характеризуется точность применённого способа измерений, следует указывать погрешность.

0ПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА И ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ.

Ранее с помощью таблицы 3.1 определялись доверительные вероятности для отдельного измерения х_i. Очевидно, важнее знать, насколько может уклоняться от истинного значения Х среднее арифметическое ряда измерений. Для этого также нужно воспользоваться данными таблицы 3.1, но вместо величины σ  необходимо взять, т.е., а величину ε определим, как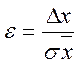     

Таким образом,  мы теперь знаем, как определять доверительную вероятность для любого доверительного интервала, если известна среднеквадратичная погрешность σ. Однако на практике в процессе измерений можно определить только величину S_П соответствующую определенному, но всегда сравнительно небольшому числу измерений n. Если для оценки доверительной вероятности будем считать, что полученное значение S_П совпадает с величиной σ, и будем пользоваться таблицей 3.1. для нахождения доверительной вероятности, то найдем неверные /завышенные/ значения α. Это результат того, что при определении среднеквадратичной погрешности из малого числа наблюдений мы находим последнюю с малой точностью, что приводит к невысокой надежности полученного результата. Стьюдент /псевдоним английского математика В.С.Госсета/ указал на возможность и при ограниченном количестве измерений определять доверительный интервал для любой доверительной вероятности.

По Стьюденту, границу доверительного интервала для доверительной вероятности α можно представить в виде

,

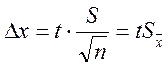где t - коэффициент Стьюдента;- оценка среднего квадратического отклонения среднеарифметического.

Коэффициент Стьюдента /см. таблицу 5.1/ зависит от доверительной вероятности и  числа измерений.

Таблица 5.1