Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 14

экспериментальные данные так, чтобы по возможности точно отразить общую тенденцию зависимости У от Х, но вместе с тем  сгладить незакономерные, случайные

 уклонения, связанные с не­избежными погрешностями измерений, т.е. требуется выбрать коэффициен­ты полинома так,  чтобы зависимость ¦(х) в каком-то смысле наилучшим образом изображала зависимость, полученную в опыте.

Решение этой задачи зависит оттого, что именно условиться считать "наилучшим". Можно, например, считать "наилучшим" такое взаимное рас­положение кривой и экспериментальных точек, при котором максимальное расстояние между ними обращается в минимум; можно потребовать, чтобы в минимум обращалась сумма абсолютных отклонений точек от кривой и т.д. При каждом из этих требований получим свое решение задачи, свои значе­ние параметров bi; Однако общепринятым при решении подобных задач является так на­зываемый метод наименьших квадратов, при котором требование наилучше­го согласования кривой ¦(х) и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от аппроксимирующего полинома обращалась в минимум.

Рис.2 Аппроксимация опытов

Метод наименьших квадратов имеет существенные преимущества пе­ред другими методами: во-первых, он приводит к сравнительно простому ма­тематическому способу определения коэффициентов Bi;  во—вторых, он до­пускает достаточно веское теоретическое обоснование с вероятностной точки зрения.

 Предположим, что истинная зависимость Y от Х в точности выражает­ся формулой j(X). Экспериментальные точки уклоняются от этой зависимо­сти вследствие неизбежных ошибок измерения. Напомним, что в большинст­ве практических случаев ошибки измерения подчиняются нормальному зако­ну. Рассмотрим какое-либо значение фактора Xi. Результат опыта есть случайная величина функции отклика YI, распределенная по нормальному зако­ну с математическим ожиданием j(хi) и со средним квадратичным отклоне­нием si  характеризующим ошибку измерения. Предположим, что точность измерения во всех точках одинакова:

Тогда нормальный закон, по которому распределяется величина   можно записать в виде

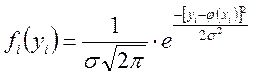
В результате измерений случайные величины  приняли  совокупность  значений . Необходимо подобрать математические ожидания так, чтобы вероятность этого события была максимальной (прин­цип максимального правдоподобия).

Строго говоря, вероятность любого из событий    равна нулю, так как величины  непрерывны, поэтому воспользуемся не вероятностями со­бытий , а соответствующими элементами вероятностей:

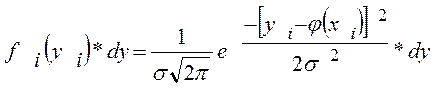
Найдем вероятность того, что система случайных величин примет со­вокупность значений,  лежащих в пределах:

 

Так как опыты независимы, эта вероятность равна произведению эле­ментов вероятностей для всех i:

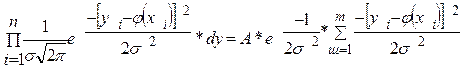  (2)

где А - некоторый коэффициент, независящий от .

Требуется так  выбрать математические ожидания ,  чтобы выражение (2) обращалось в максимум.

Величина:

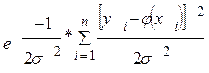
всегда меньше единицы, поэтому, очевидно, что она имеет наибольшее зна­чение, когда показатель степени по абсолютной величине минимален.

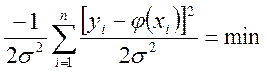
Отбрасывая постоянный множитель, 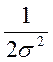       получаем требование метода

наименьших квадратов: для того, чтобы данная совокупность опытных зна­чений  была наивероятнейшей, нужно выбрать функцию так, чтобы сумма квадратов отклонений опытных значений     от   была минимальной:

Перейдем к задаче определения параметров  исходя из прин­ципа наименьших квадратов. Пусть  имеется  ряд  экспериментальных  данных и из каких-то соображений (связанных с существом явления или с внешним   видом  наблюдаемой зависимости) выбран общий вид функции у = j(х), зави­сящей от нескольких числовых параметров .

Запишем функцию у  как функцию не только аргументов, но и пара­метров :      

.

Требуется выбрать , так, чтобы соблюдалось условие:

Найдем,  значения  обращая левую часть выражения в минимум. Для того продифференцируем ее по  и приравняем производные к нулю: