Общие сведения и классификация измерений. Погрешности измерений. Необходимое число измерений. Порядок операций при обработке экспериментальных данных прямых измерений. Построение планов полного факторного эксперимента. Свойства матриц планирования, страница 18

Каждый коэффициент линейной модели равен изменению функции отклика при переходе соответствующего фактора с нулевого уровня на верх­ний, т.е. роль данного фактора тем больше, чем больше абсолютная величина коэффициента. Изменение величины функции отклика при переходе фактора с нижнего уровня на верхний равно удвоенному коэффициенту в уравнении регрессии, стоящему перед этим фактором, и называют "эффектом фактора" или "основным эффектом''.

Не всегда в выбранных интервалах варьирования удается получить ли­нейную модель. Один из наиболее часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором нахо­дится другой фактор. В этом случае имеет место эффект взаимодействия двух  факторов.

Полный факторный эксперимент позволяет получить количественную оцен­ку эффекта взаимодействия. При добавлении вектор - столбцов эффектов взаимодействия все рассмотренные свойства матриц планирования сохраня­ются, поэтому для линейной модели:

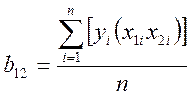
Рассмотрим на численном примере двухфакторного эксперимента про­цесс определения основных эффектов и эффекта взаимодействия. Аппрокси­мирующая функция (уравнение регрессии) изучаемого процесса на основе априорной информации представлена в виде

После выбора интервалов варьирования и кодирования факторов со­ставлена матрица планирования полного факторного эксперимента и прове­дено четыре опыта для определения коэффициентов регрессии. Численные значения опытов приведены в матрице планирования.

Таблица 4 Матрица планирования двухфакторного эксперимента
N опыта		«
1.	+1	+1	+1	+1	93,2
2.	+1	-1	+1	-1	88,7
3.	+1	+1	-1	-1	82,9
4.	+1	-1	-1	+1	81,2

Легко видеть, что матрица планирования сохранила свои основные свойства. Из этого следует, что

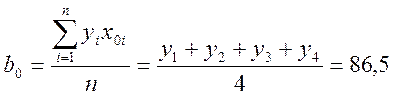
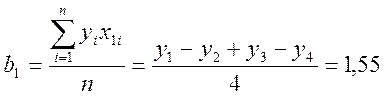
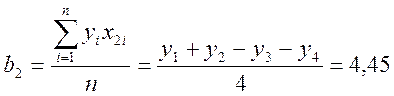
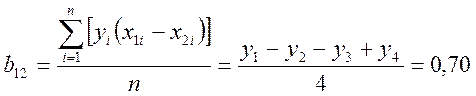
Таким образом, уравнение математической модели будет выглядеть как

у=86,5 +1,55 +4.45+0.70

С ростом числа факторов число возможных взаимодействий быстро растет. В двухфакторном эксперименте возможно только одно взаимодействие (эффект взаимодействия первого порядка), а в трехфакторном три парных эффекта взаимодействия: и один тройной эффект (эффект  взаимодействия второго порядка):.

Число возможных взаимодействий какого-либо порядка определяется формулой для числа сочетаний из L элементов (факторов) по  т  (взаимодей­ствующих факторов):

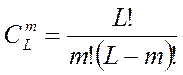
По принятой терминологии  - число взаимодействии (m-1) - ого по­рядка.  Например, для пятифакторного эксперимента (план 2⁵) число парных взаимодействий равно десяти

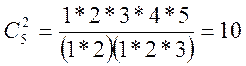
Количество коэффициентов в уравнении, содержащем свободный член, основные эффекта и все возможные эффекта взаимодействия, равно числу опытов полного факторного эксперимента.

Как указывалось выше, ортогональность матриц планирования приво­дит к тому, что оценки коэффициентов независимы друг от друга. Это важ­ное преимущество полного факторного эксперимента и других матриц пла­нирования, сохранявших свойство ортогональности. Но такую независимую оценку нельзя получить для коэффициентов при квадратичных или кубических членах.

Например, попытка построения вектор - столбцов  приво­дит к получению столбцов, совпадающих друг с другом для разных факторов так как  = 1. Величина коэффициента  в этом случае складывается из ис­тинного значения свободного члена    и вкладов квадратичных членов

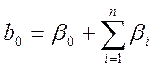
т.е.  имеет  место  смешанная  оценка  свободного и  квадратичных  членов.