Приведем примеры пользования результатами
таблицы. Пусть для некоторого ряда измерений получили ![]() =20,
σ =2. Какова вероятность того, что результат отдельного измерения не выйдет за
пределы, определяемые равенством 17 < хi < 23?
Доверительные границы равны ± 3, что составляет в долях σ -1,5. Из таблицы 3.1
находим, что доверительная вероятность для ε = 1,5 равна 0,87. Иначе говоря,
87% всех измерений уложится в интервал погрешности ± 3 .
=20,
σ =2. Какова вероятность того, что результат отдельного измерения не выйдет за
пределы, определяемые равенством 17 < хi < 23?
Доверительные границы равны ± 3, что составляет в долях σ -1,5. Из таблицы 3.1
находим, что доверительная вероятность для ε = 1,5 равна 0,87. Иначе говоря,
87% всех измерений уложится в интервал погрешности ± 3 .
Сформулируем вторую задачу, какой доверительный интервал нужно выбрать для тех же измерений, чтобы 99% результатов попала в него? По таблице 3.1 находим, что значению α =0,99 соответствует значение ε =2.6, следовательно, доверительный искомый интервал равен Δх = ε*σ = 2,6* 2=5,2.
Таким образом, для нахождения случайной погрешности нужно определи два числа - доверительный интервал /величину погрешности/ и доверительную вероятность. Средней квадратичной погрешности σ соответствует доверительная вероятность 0.68, удвоенной средней квадратичной погрешности 2σ - доверительная вероятность 0.95; утроенной /Зσ/ - 0.997.
Приведенные три значения α полезно запомнить, так как обычно в литературе дается значение средней квадратичной погрешности и не указывается соответствующая ей доверительная вероятность.
Наряду со среднеквадратичной погрешностью иногда используется погрешность среднеарифметическая, вычисляемая по формуле
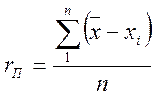 ;
; ![]()
При большом числе наблюдений rп и SП существуют простые соотношения
SП =1.25 rП; rП = 0.80 SП
Известным преимуществом средней арифметической погрешности является сравнительно простой способ ее вычисления. Если пользоваться средней арифметической погрешностью и при малой n, то правильнее ее вычислять по соотношению
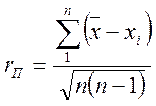
СЛОЖЕНИЕ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
Предположим, что измеряемая величина Z
является суммой /или разностью/ двух величин Х и Y, результаты измерений
которых независимы. Тогда, если ![]() ,
,![]() -
дисперсия величин Х и Ү, то дисперсия измеряемой величины
-
дисперсия величин Х и Ү, то дисперсия измеряемой величины ![]() будет равна
будет равна
![]() =
=![]() +
+![]() или
или ![]() =
= ![]()
Если Z является суммой не двух, а большего числа слагаемых - закон сложения погрешностей будет таким же.
Таким образом, средняя квадратичная погрешность суммы /ила разности/ нескольких независимых величин равна корню квадратному, из суммы дисперсий отдельных слагаемых. Необходимо твердо помнить, что для нахождения суммарной погрешности нужно складывать не сами погрешности, а их квадраты и извлечь квадратный корень.
Из закона сложения погрешностей следует
два важных вывода. Первый из них относится к роли каждой из погрешностей в
общей погрешности результата. Поясним сказанное на примере: пусть Х и Y два
слагаемых, определенных со средней квадратичной погрешностью ![]() и
и ![]() , причем
, причем
![]() в два раза меньше
в два раза меньше![]() .
Тогда ошибка суммы будет
.
Тогда ошибка суммы будет
![]() =
=![]() +
+![]() =
=![]() +
+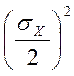 ;
;
![]()
Иначе говоря, если одна из ошибок в два раза меньше другой, то общая погрешность возросла за счет меньшей из погрешностей всего на 10%. Это означает, что если необходимо повысить точность измерения величины Z, то нужно в первую очередь стремиться уменьшить ту погрешность измерения, которая больше. Если оставить точность измерения Х неизменной, то, как бы мы не повышали точность измерения Y, погрешность конечного результата не удастся уменьшить более чем на 10%. Этот вывод нужно иметь в виду и при повышении измерений в первую очередь уменьшать погрешность, имеющую наибольшую величину.
Второй вывод, вытекающий из закона сложения погрешностей, относится к определению погрешности среднего арифметического. Среднее арифметическое оточено меньшей ошибкой, чем результат каждого отдельного измерения. Покажем это. Пусть х1,х2,…,хn - результаты отдельных измерений, каждое из которых характеризуется дисперсией σ². Среднее арифметическое всех измерений можно представить в виде
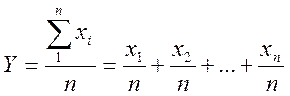
В соответствии с законом сложения погрешностей дисперсию величины Y можно найти как
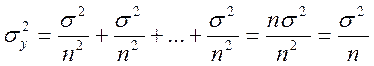
Но Y и есть среднее арифметическое из всех величин хi, поэтому
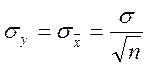
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.