Отметим, что, не имея строгого решения, вопрос о правилах сложения систематической и случайной погрешностей решается разным образом. Одно из возможных правил, нашедших широкое практическое применение, заключается в том, что распределение систематической погрешности происходит также по нормальному закону, а указанная величина этой ошибки δ соответствует утроенному значению средней квадратичной погрешности.
Исходя из вышесказанного, можно выделить три типичных случая, возникающих при обработке экспериментальных данных прямых измерений:
4. Если значение систематической погрешности / погрешности аппаратуры/ значительно больше значения случайной погрешности, то измерение следует проводить один раз. В этом случае граница доверительного интервала при доверительной вероятности α определяется формулой
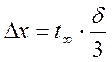
где t – коэффициент Стьюдента при n →∞ и заданной α.
В частности, для α = 0.95 доверительные интервалы равны соответственно
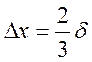 ,
,
2. Если значение систематической погрешности прибора соизмеримо с погрешностью отсчитывания, то доверительный интервал при доверительной вероятности α равен
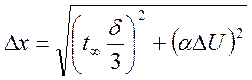
для α = 0.95 соответственно имеем
![]()
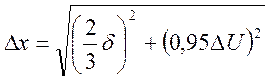
3. Если случайная погрешность значительно больше инструментальной, измерение необходимо выполнить несколько раз /см. раздел 6/. Граница овериительного интервала погрешности для доверительной вероятности α определяется по формуле
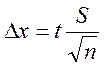 ,
,
где t – коэффициент Стьюдента при заданных n и α, S – среднеквадратичное отклонение метода измерения.
При точных измерениях нужно произнести такое количество измерении, чтобы случайная погрешность, определяемая величиной S, стала значительно меньшей систематической погрешности и чтобы последняя снова определяла окончательную погрешность измерения.
4. Если случайная погрешность сравнима с инструментальной /систематической/, то оценивается влияние обеих погрешностей. В этом случае границу доверительного интервала погрешности измерения для овериительной вероятности α находят по формуле
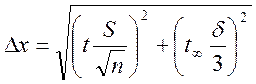
В двух последних случаях погрешность отсчитывания можно учесть, используя закон сложения случайных погрешностей.
Лекция 3.
П0РЯДОК ОПЕРАЦИЙ ПРИ ОБРАБОТКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРЯМЫХ ИЗМЕРЕНИЙ.
Пусть выполнено n измерений величины х -
с помощью прибора, имеющего систематическую погрешность δ. Необходимо найти
среднюю величину ![]() и доверительный интервал Δх при
доверительной вероятности α.
и доверительный интервал Δх при
доверительной вероятности α.
1. В общем случае на первом этапе необходимо произвести проверку нормальности распределения случайных погрешностей. Обычно задача ставится так: имеется группа результатов наблюдений и высказывается гипотеза, что эти наблюдения можно считать реализациями случайной величины с нормальным законом распределения. Для решения этой задачи в статистике разработан ряд критериев, например, критерий К.Пирсона, критерии Р.Назема - Н.В.Смирнова и др. Но, как указывалось выше, подавляющему большинству измерений, выполняемых при технических исследованиях, соответствует нормальный закон распределения погрешностей. Поэтому в дальнейшем будем считать гипотезу о нормальном распределение погрешностей выполненной.
2. Вычисляем наиболее вероятное среднее арифметическое значение
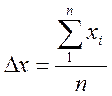
3. Вычисляем оценку среднеквадратического отклонения результата отельного наблюдения
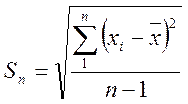
4. Проверяем результаты наблюдений на наличие грубых погрешностей. С этой целью для измерений наиболее отличающихся от среднего значения, определяем величину
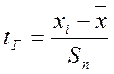
Выбираем уровень значимости q /1 ÷ 5%/ и по таблице 7.1 определяем значение t тг. Если t г > t гт величина отбрасывается и повторно вычисляется
величина среднего арифметического и оценка среднего квадратического отклонения. Если t г < t гт измерение оставляем.
5. Вычисляем оценку среднеквадратического отклонения среднего арифметического:
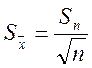
6. Производим оценку погрешности считывания.
7. Сравниваем полученное значение случайной погрешности с систематической и, если случайная погрешность значительно больше / в три-пять раз/ систематической, граница доверительного интервала при доверительной вероятности α равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.