Основы электростатики. Изучение электрического поля, страница 19

,

где  - угол между вектором  и внешней нормалью  к положительно заряженной поверхности диэлектрика,  - толщина пластины,  - расстояние между основаниями цилиндров. Объем  имеет электрический момент

,

где  - модуль вектора поляризации. Этот объем эквивалентен диполю, образованному зарядами  и , отстоящими друг от друга на расстояние . Его электрический момент , тогда , и

                    (1.2.5)

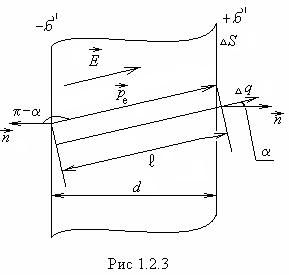
где  - составляющая вектора поляризации по внешней нормали к соответствующей поверхности. Для правой поверхности (рис.1.2.3) , поэтому , для левой  и . Известно, что , тогда

                                                                      (1.2.6)

где  - нормальная составляющая напряженности поля внутри диэлектрика.

Из формулы (1.2.6) следует, что, если  - линии напряженности выходят из диэлектрика, то на поверхности появляются положительные связанные заряды . Если  - линии напряженности входят в диэлектрик, то на поверхности появляются отрицательные заряды .Формулы (1.2.5) и (1.2.6) справедливы и в общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле.

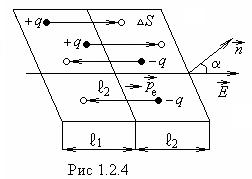           Найдем объемную плотность связанных зарядов, возникающих внутри неоднородного диэлектрика. В неоднородном изотропном диэлектрике с неполярными молекулами рассмотрим воображаемую малую площадку (рис 1.2.4). Пусть в единице объема диэлектрика имеется n одинаковых частиц с зарядом -  и  одинаковых частиц с зарядом . В небольшой окрестности  поле и диэлектрик можно считать однородными. Поэтому при включении поля все положительные заряды, находящиеся вблизи , сместятся в направлении  на расстояние , а отрицательные - противоположно  на  расстояние . При этом через площадку  пройдет в направлении нормали к ней некоторое количество зарядов одного знака (положительных, если , или отрицательных, если).