Основы электростатики. Изучение электрического поля, страница 32

1.4.1.ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА

       Будем считать среду, в которой находятся электрические заряды и заряженные тела, однородной и изотропной, не обладающей сегнетоэлектрическими свойствами.

       Заряжая некоторый проводник, необходимо совершить определенную работу против кулоновских сил отталкивания между одноименными электрическими зарядами. Эта работа идет на увеличение электрической энергии заряженного проводника, которая в данном случае аналогична потенциальной энергии в механике.

       Рассмотрим проводник, имеющий электроемкость , заряд  и потенциал . Работа, совершаемая против сил электростатического поля при перенесении заряда  из бесконечности на проводник равна

.

       Для того, чтобы зарядить тело от нулевого потенциала до потенциала , необходимо совершить работу

.

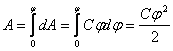Ясно, что энергия заряженного тела равна той работе, которую нужно совершить,  чтобы зарядить это тело:

.

Энергию  называют собственной энергией заряженного тела. Ясно, что собственная энергия есть не что иное, как энергия электростатического поля этого тела

.

1.4.2.ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА

       Пусть потенциал обкладки конденсатора, на которой находится заряд , равен , а потенциал обкладки, на которой находится заряд , .

       Энергия такой системы зарядов равна:

, то есть

равна собственной энергии системы зарядов, где  - напряжение между обкладками конденсатора, .

Рассмотрим плоский конденсатор. Энергия, заключенная в единице объема электростатического поля называется объемной плоскостью энергии. Эта объемная плоскость должна быть одинаковой во всех точках однородного поля, а полная энергия поля пропорциональна его объему. Известно, что , , тогда для энергии имеем:

,

но  - объем электростатического поля между обкладками конденсатора, то есть

.

Тогда объемная плотность энергии  однородного электростатического поля конденсатора равна

,

то есть определяется его напряженностью или смещением. В случае неоднородных электрических полей

.

Найдем энергию сферического конденсатора. На расстоянии  от центра заряженного шара напряженность его электростатического поля равна

.

Рассмотрим бесконечно тонкий шаровой слой, заключенный между сферами радиусов  и . Объем такого слоя: