Основы электростатики. Изучение электрического поля, страница 10

,

причем  - заряд, заключенный внутри объема  (ввиду малости  можно считать что  внутри параллелепипеда всюду одинакова),

,

тогда

,

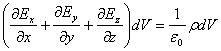или

Сумма, стоящая в левой части, называется дивергенцией вектора ,

, или

-дивергенция вектора напряженности равна объемной плотности зарядов, создающих поле, деленной на . Это выражение представляет собой теорему Гаусса в дифференциальной форме. Она характеризует поле в точке. Электрические заряды являются источниками и стоками поля вектора . Линии вектора  начинаются и заканчиваются на электрических зарядах. Если  - это источник поля , если  - сток поля. Если , то в данной точке нет зарядов, линии  не прерываются.

1.1.8.ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА К РАСЧЕТУ ПОЛЕЙ

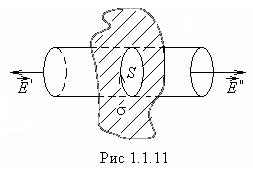
     1.Найдем напряженность электрического поля бесконечной нити, заряженной с линейной плотностью заряда (рис.1.1.10). Построим гауссову поверхность в виде цилиндра, ось которого совпадает с нитью. Радиус цилиндра r, высотаh . В силу симметрии рассматриваемого поля линии вектора напряженности  расходятся радиально от нити, и поток вектора  отличен от нуля только через боковую поверхность цилиндра:

Очевидно, на одинаковом расстоянии r от нити значения Е будут одинаковы, поэтому  Согласно теореме Гаусса

где - заряд, заключенный внутри гауссова цилиндра. Тогда

и     - напряженность поля заряженной нити на расстоянии  r от  нее.

2.  Поле бесконечной однородной заряженной плоскости. Поверхностная плотность заряда  во всех точках плоскости одинакова . Напряженность поля перпендикулярна к плоскости. В симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению. Построим цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями  (рис.1.1.11). В силу симметрии .

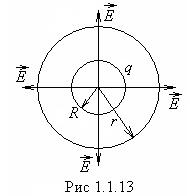
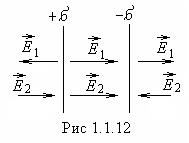Поток через боковую поверхность равен нулю, так как вектор  перпендикулярен к этой поверхности, таким образом суммарный поток через поверхность цилиндра равен  , и     .