1.2.8.УСЛОВИЯ НА ГРАНИЦЕ ДВУХ ДИЭЛЕКТРИКОВ
 Можно показать, что линии смещения при переходе через границу
диэлектриков не претерпевают разрыва. Поместим в однородное поле
Можно показать, что линии смещения при переходе через границу
диэлектриков не претерпевают разрыва. Поместим в однородное поле ![]() две сложенные вместе плоскопараллельные
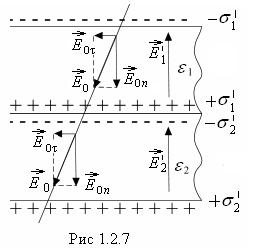
пластины из разных диэлектриков (рис.1.2.7). Сторонних зарядов на границе
раздела нет. Возникшие на поверхностях пластин связанные заряды создают внутри
каждой пластины перпендикулярное к ее поверхностям поле
две сложенные вместе плоскопараллельные
пластины из разных диэлектриков (рис.1.2.7). Сторонних зарядов на границе
раздела нет. Возникшие на поверхностях пластин связанные заряды создают внутри
каждой пластины перпендикулярное к ее поверхностям поле ![]() .
В первой пластине напряженность этого поля равна
.
В первой пластине напряженность этого поля равна ![]() ,
во второй
,
во второй ![]() . В сумме с нормальной составляющей
напряженности поля свободных зарядов
. В сумме с нормальной составляющей
напряженности поля свободных зарядов ![]() вектор
вектор
![]() дает нормальную составляющую результирующего
поля в пластинах. Векторы
дает нормальную составляющую результирующего
поля в пластинах. Векторы ![]() и
и ![]() коллинеарны, поэтому нормальные
составляющие вектора напряженности в диэлектриках соответственно равны:
коллинеарны, поэтому нормальные
составляющие вектора напряженности в диэлектриках соответственно равны:
![]() (1.2.15)
(1.2.15)
В
направлении касательной к поверхности раздела никакого дополнительного поля не
создается, поэтому тангенциальная составляющая вектора ![]() при
переходе через границу не меняется:
при
переходе через границу не меняется:
![]() . (1.2.16)
. (1.2.16)
Поверхностная плотность связанных зарядов, как следует из выражения (1.2.6), определяется нормальной составляющей результирующего поля в данной пластине:
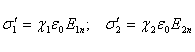 .
.
Подставив
![]() и
и ![]() в
формулу (1.2.15), имеем
в
формулу (1.2.15), имеем
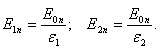 (1.2.17)
(1.2.17)
Из выражений (1.2.16) и (1.2.17) следует, что при переходе через границу раздела двух диэлектриков нормальная составляющая напряженности поля изменяется скачком ( терпит разрыв), а тангенциальная составляющая остается без изменений.
Умножим выражения (1.2.16) и (1.2.17) на ![]() и
и
![]() соответственно, получаем
соответственно, получаем
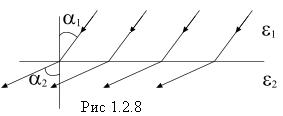
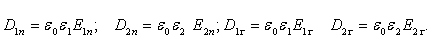 (1.2.18)
(1.2.18)
Из
формул (1.2.18) видно, что при переходе через границу раздела диэлектриков
тангенциальная составляющая вектора ![]() меняется качком,
а нормальная составляющая остается без изменений:
меняется качком,
а нормальная составляющая остается без изменений:
![]() (1.2.19)
(1.2.19)
Это равенство указывает на непрерывность линий смещения. Действительно,
количество линий электрического смещения, пронизывающих площадку ![]() , равно
, равно ![]() ,
следовательно, к площадке, расположенной на границе раздела диэлектриков,
приходит из первого диэлектрика количество линий
,
следовательно, к площадке, расположенной на границе раздела диэлектриков,
приходит из первого диэлектрика количество линий ![]() .
От этой же площадки уходит во второй диэлектрик количество линий
.
От этой же площадки уходит во второй диэлектрик количество линий ![]() . Так как
. Так как ![]() ,
то и
,
то и ![]() . Таким образом, линии электрического
смещения не заканчиваются и не начинаются на границе раздела, т.е. проходят через
нее, не претерпевая разрыва при условии, что на границе раздела нет сторонних
зарядов.
. Таким образом, линии электрического
смещения не заканчиваются и не начинаются на границе раздела, т.е. проходят через
нее, не претерпевая разрыва при условии, что на границе раздела нет сторонних
зарядов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.