![]() .
.
 Этот заряд равен
Этот заряд равен ![]() , где
, где ![]() - объемная плотность связанных зарядов. Интеграл
бёрется по объему
- объемная плотность связанных зарядов. Интеграл
бёрется по объему ![]() , ограниченному поверхностью
, ограниченному поверхностью ![]() . Тогда
. Тогда
![]() .
.
Применим к этому выражению
теорему Стокса, получаем: ![]() , или
, или
![]() (1.2.9)
(1.2.9)
- объемная плотность
связанных зарядов равна дивергенции вектора ![]() , взятой с обратным знаком.
, взятой с обратным знаком.
Точки с![]() (рис. 1.2.5) служат источниками поля вектора
(рис. 1.2.5) служат источниками поля вектора ![]() , из этих точек линии вектора
, из этих точек линии вектора ![]() расходятся.
Точки с
расходятся.
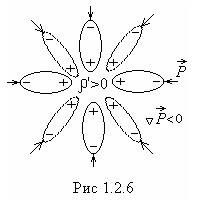
Точки с ![]() (рис.1.2.6) служат стоками поля вектора
(рис.1.2.6) служат стоками поля вектора ![]() , к этим точкам линии
, к этим точкам линии ![]() сходятся.
При поляризации диэлектрика положительные связанные заряды смещаются в
направлении вектора
сходятся.
При поляризации диэлектрика положительные связанные заряды смещаются в
направлении вектора ![]() , а отрицательные связанные заряды - в
противоположном. В результате в местах с положительной дивергенцией
, а отрицательные связанные заряды - в
противоположном. В результате в местах с положительной дивергенцией ![]() образуется избыток отрицательных связанных зарядов, а в местах с
отрицательной
образуется избыток отрицательных связанных зарядов, а в местах с
отрицательной ![]() - избыток положительных связанных зарядов.
- избыток положительных связанных зарядов.
Связанные заряды отличаются
от сторонних лишь тем, что не могут покинуть пределы молекул, в состав которых
они входят. В остальном их свойства не отличаются от свойств других зарядов.
Поэтому, если плотность связанных зарядов ![]() отлична от нуля, теорему Гаусса для вектора
отлична от нуля, теорему Гаусса для вектора ![]() следует писать в виде:
следует писать в виде:
![]() ,
(1.2.10)
,
(1.2.10)
тогда уравнение Пуассона принимает вид
![]() ,
,
где ![]() - плотность сторонних (свободных) зарядов.
- плотность сторонних (свободных) зарядов.
Из (1.2.9) имеем
![]()
или ![]() , и
, и
![]() .
(1.2.11)
.
(1.2.11)
Из выражения (1.2.11) следует, что
объемная плотность связанных зарядов может быть отлична от нуля в двух случаях:
- если диэлектрик неоднороден, ![]() ; и, - если в данном месте диэлектрика плотность сторонних зарядов
отлична от нуля,
; и, - если в данном месте диэлектрика плотность сторонних зарядов
отлична от нуля, ![]() .
.
Если внутри диэлектрика сторонних (свободных) зарядов нет, имеем:
![]() .
.
ЛЕКЦИЯ 5
1.2.5. ВЕКТОР ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ
Источниками электрического поля служат не только сторонние, но и связанные
заряды, т.е. ![]() , или
, или ![]() . Раскрыв скобки и сгруппировав,
получаем:
. Раскрыв скобки и сгруппировав,
получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.