Основы электростатики. Изучение электрического поля, страница 33

.

Энергия слоя  следовательно,  

.

Тогда полная энергия заряженного шара равна: 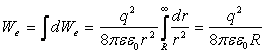, где  - радиус шара. Емкость шара , следовательно,  - энергия электростатического поля сферического конденсатора равна его собственной энергии, так как заряженное тело потому и обладает электрической энергией, что при его зарядке была совершена работа против сил создаваемого им электростатического поля.

1.4.3.ЭНЕРГИЯ ПОЛЯРИЗОВАННОГО ДИЭЛЕКТРИКА

       Рассмотрим однородный изотропный диэлектрик, находящийся во внешнем электрическом поле. Процесс поляризации  связан с работой по деформации электронных орбит в атомах и молекулах и по повороту осей молекул-диполей вдоль поля. Ясно, что поляризованный диэлектрик должен обладать запасом электрической энергии.

       Если поле напряженностью  создано в вакууме, , то объемная плотность энергии этого поля в точке с напряженностью  равна:

Докажем, что объемная плотность энергии поляризованного диэлектрика в этой точке выражается формулой:

.

Рассмотрим диэлектрик с неполярными молекулами. Молекулы такого диэлектрика являются упругими диполями. Электрический момент упругого диполя, находящегося в поле с напряженностью , равен , где  - поляризуемость диполя.

Или в скалярной форме:

                                      (1.4.1)

 - заряд и плечо диполя.

       На заряд  со стороны поля действует сила , которая при увеличении длины диполя на  совершает работу

.

Из выражения (1.4.1) получаем: ,

поэтому

.                                                       (1.4.2)

       Чтобы найти работу  поля при деформации одного упругого диполя, надо проинтегрировать выражение (1.4.2):

.

Работа  равна той потенциальной энергии, которой обладает упругий диполь в электрическом поле напряженностью . Пусть  - число диполей в единице объема диэлектрика. Тогда потенциальная энергия всех этих диполей, то есть объемная плотность энергии поляризованного диэлектрика равна:

.

Однако  - модуль вектора поляризации, тогда . Известно, что , и , тогда  , что и требовалось доказать.