Основы электростатики. Изучение электрического поля, страница 5

,                                    (1.1.1)

но известно , что  ; и , где - напряженность результирующего поля;  - напряженность поля, создаваемого одним зарядом .

Тогда  (выражение (1.1.1) разделили на ) - напряженность электрического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности.

       Таким образом, результирующее поле можно найти простым наложением (суперпозицией) полей отдельных зарядов. В этом и состоит принцип суперпозиции полей, или принцип независимых действий электрических полей.

       Пусть  - радиус-вектор, проведенный из точечного заряда  в исследуемую точку поля. Тогда напряженность, создаваемая этим зарядом в данной точке поля , а результирующая напряженность .

       Каждое заряженное тело можно разбить на столь малые части, что каждая из них будет представлять собой точечный заряд. Поэтому формула эта пригодна для расчета любых электрических полей.

1.1.5. Примеры расчета полей на основе

принципа суперпозиции.   Поле электрического диполя

Электрическим диполем называется система равных по величине и противоположных по знаку электрических зарядов  и , расстояние  между которыми мало по сравнению с расстоянием до рассматриваемых точек поля.

       Молекулы диэлектриков по своим свойствам подобны диполям.

       Плечом диполя называется вектор , направленный по оси диполя от отрицательного заряда к положительному и численно равен расстоянию между ними. Произведение положительного заряда диполя  на плечо  называется электрическим моментом диполя :

.

Вектор  совпадает по направлению с плечом диполя .

       Согласно с принципом суперпозиции полей напряженность  в произвольной точке диполя равна

,

где  и   - напряженности полей зарядов  и   соответственно.

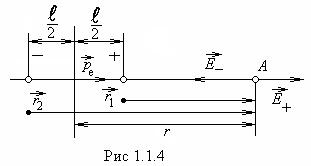
1.Если точка  расположена на оси диполя (рис.1.1.4), то векторы  и  направлены вдоль этой оси в противоположные стороны,

,  ,

где  и  - радиус-векторы, проведенные в точку  из концов диполя  и ,    ; . Векторы  и  совпадают по направлению с , поэтому: