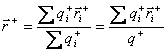Основы электростатики. Изучение электрического поля, страница 16

,

где- радиус-вектор точки, в которой появляется -ый положительный заряд   - суммарный положительный заряд молекулы.

Радиус-вектор центра тяжести отрицательных зарядов равен:

.

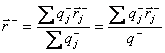Ясно, что суммарный  положительный заряд молекулы равен суммарному отрицательному заряду, взятому с обратным знаком.

В отсутствие внешнего электрического поля центры положительных и отрицательных зарядов могут совпадать (молекула неполярна), либо не совпадать (молекула полярна, эквивалентна электрическому диполю). Полярная молекула обладает собственным электрическим моментом.

.

Если для положительных  и отрицательных зарядов применить единую нумерацию, то

                                   .                                                       (1.2.1)

Если система зарядов в целом нейтральна, то выражение (1.2.1) не зависит от выбора точки, относительно которой берутся радиус-векторы. Неполярные молекулы собственным электрическим моментом не обладают. Под действием внешнего электрического поля заряды в неполярной молекуле смещаются друг относительно друга: положительные по направлению поля, отрицательные - против поля. В результате молекула приобретает электрический момент, пропорциональный напряженности поля:

где  - поляризуемость молекулы.

Явление, заключающееся в возникновении в каждом объеме диэлектрика макроскопического электрического дипольного момента, называется поляризацией.

           Процесс поляризации неполярной молекулы можно объяснить, если представить, что положи­тельные и отрицательные заряды молекулы связаны друг другом силами, пропорциональными их смещению, то есть  неполярная: молекула ведет себя как упругий диполь.

            Действие внешнего поля на полярную молекулу сводится к стремлению повернуть молекулу так, чтобы ее электрический момент установился по направлению поля. На величину же электрического момента внешнее поле практически не влияет, то есть молекула ведет себя как жесткий диполь.

1.2.2. ДИПОЛЬ В ОДНОРОДНОМ И НЕОДНОРОДНОМ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ

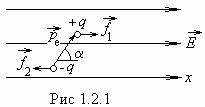
Если диполь поместить в однородное электрическое поле, то на заряды диполя  и  будут действовать равные по величине и проти­воположные по направлению силы  и  (рис 1.2.1). Эти силы обра­зуют  пару, плечо которой равно , т.е. зависит от ориентации диполя в поле. Модуль каждой силы  равен . Момент пары сил

,

где  - электрический момент диполя. Переходя к векторной форме записи, получаем:           .                                          

Момент  стремится повернуть диполь так, чтобы его момент  установился по направлению поля.

                Чтобы увеличить угол между векторами  и  на , нужно совершить работу  против сил, действующих  на диполь в электрическом поле: