Основы электростатики. Изучение электрического поля, страница 6

; ,

тогда , ,

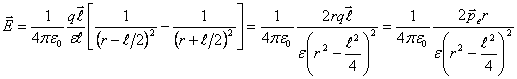Если , то .

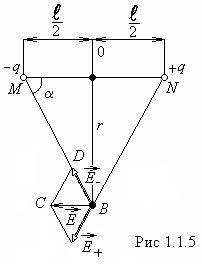
2. Найдем напряженность поля диполя в точке , расположенной на перпендикуляре, восстановленном к оси диполя из его середины (рис.1.1.5.). Точка равноудалена от зарядов и , поэтому:

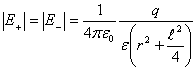
Из подобных треугольников и получаем, что вектор антипараллелен вектору электрического момента диполя :

Модуль напряженности ,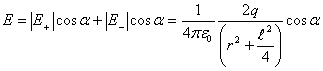

ясно, что , .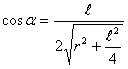

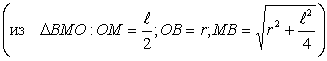Тогда 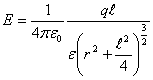. Величина , ею можно пренебречь, поэтому

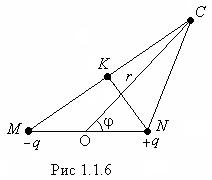
3. В общем случае пусть точка лежит на расстоянии от середины диполя, радиус-вектор образует с осью диполя угол (рис.1.1.6).

Опустим из точки перпендикуляр на . Поместим в точку два точечных заряда и (равных по величине зарядам диполя). Эти заряды компенсируют друг друга и не искажают поле диполя. Четыре заряда, находящихся в точках можно рассматривать как два диполя и , , поэтому . Поэтому электрические моменты диполей соответственно равны: