Основы электростатики. Изучение электрического поля, страница 13

       Очевидно, сумма потенциальных полей тоже есть потенциальное поле (так как если работа слагаемых сил не зависит от формы пути, то и работа равнодействующей от нее не зависит). Поле произвольной системы зарядов можно рассматривать как сумму полей каждого из точечных зарядов, поэтому всякое электростатическое поле есть поле потенциальное.

       По определению, проекция  на произвольное направление поля  равна

,

где  - бесконечно малая площадка, проходящая через точку  перпендикулярно вектору .

Так как циркуляция вектора  по замкнутому контуру равна , , то

        ,                или      .                             (1.1.4)

Так как направление  выбрано произвольно, то проекция  на любые направления равна 0, поэтому из (1.1.4)  во всех точках электростатического поля, то есть электростатическое поле является безвихревым. Этот результат можно получить и из теоремы Стокса. Выражения (1.1.3) и (1.1.4) эквивалентны.

1.1.10.ПОТЕНЦИАЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯДА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

       Работа сил электрического поля, созданного зарядом , по перемещению заряда  из точки 1 в точку 2 равна:

.

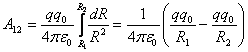Работа сил консервативного поля равна убыли потенциальной энергии:

,

тогда потенциальная энергия заряда  в поле заряда  равна:

.

       Значение константы выбирается таким, чтобы при удалении заряда на бесконечность (то есть при ) потенциальная энергия обратилась бы в ноль, поэтому

.

Ясно, что разные пробные заряды  и  в одной и той же точке поля будут обладать разной потенциальной энергией  и . Однако отношение   для всех пробных зарядов будет одинаково. Величина

называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен

.

       Если поле создается системой  точечных зарядов, то

,

где  - расстояние от заряда  до  начального положения заряда ,  - расстояние от заряда  до конечного положения заряда  (заряд  перемещается силами поля).