![]()
С другой стороны согласно теореме Гаусса,
этот поток равен ![]() , причем
, причем ![]() , если
, если ![]() . Таким
образом,
. Таким
образом, ![]() при
при ![]() и
и
![]() , то есть
, то есть ![]() при
при
![]() .
.
 Для проекции вектора
Для проекции вектора ![]() на направление радиуса имеем:
на направление радиуса имеем: ![]() . Внутри сферы при
. Внутри сферы при ![]()
![]() ; в
первой среде
; в
первой среде ![]() при
при ![]() , во второй среде
, во второй среде ![]() при
при ![]() ; за
пределами второй среды
; за
пределами второй среды ![]() при
при ![]() . Таким
образом,
. Таким
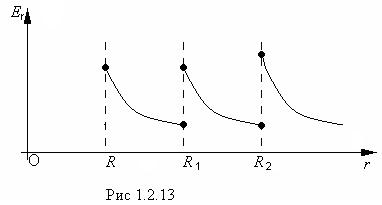
образом, ![]() терпит разрыв дважды: на границе
«первая и вторая среда» и «вторая среда - вакуум». Зависимость
терпит разрыв дважды: на границе
«первая и вторая среда» и «вторая среда - вакуум». Зависимость ![]() представлена на рис. 1.2.13.
представлена на рис. 1.2.13.
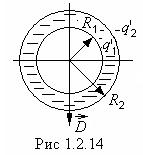
4.Поле внутри шарового слоя. Окружим
заряженную сферу концентрическим шаровым слоем из однородного диэлектрика
(рис.1.2.14). На внутренней поверхности слоя появится связанный заряд ![]() , распределенный с плотностью
, распределенный с плотностью ![]()
![]() ,
на наружной поверхности заряд
,
на наружной поверхности заряд ![]() , распределенный с
плотностью
, распределенный с
плотностью ![]()
![]() .
Знак заряда
.
Знак заряда ![]() совпадает со знаком заряда
совпадает со знаком заряда ![]() сферы, знак
сферы, знак ![]() ему
противоположен. Внутри сферы при
ему
противоположен. Внутри сферы при ![]()
![]() ; в первой среде
; в первой среде ![]() при
при ![]() , во
второй среде
, во
второй среде ![]() при
при ![]() ; за пределами второй среды
; за пределами второй среды ![]() при
при ![]() .
.
Напряженность поля внутри диэлектрика равна
![]()
и
противоположна по направлению напряженности ![]() . Напряженность
результирующего поля
. Напряженность
результирующего поля
![]() -
-
убывает
по закону ![]() . Поэтому
. Поэтому ![]() ,
где
,
где ![]() - напряженность поля в диэлектрике в
непосредственной близости к внутренней поверхности слоя, именно эта
напряженность определяет величину
- напряженность поля в диэлектрике в
непосредственной близости к внутренней поверхности слоя, именно эта
напряженность определяет величину ![]() :
:
![]()
(в каждой точке поверхности ![]() ).
Тогда
).
Тогда
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.