Основы электростатики. Изучение электрического поля, страница 15

.

Согласно правилам векторного анализа

,

тогда

 - это дифференциальное уравнение называется уравнением Пуассона.

       Для участков поля, где нет электрических зарядов

 , или .

Это частный вид уравнения Пуассона – уравнение Лапласа.            Уравнение Пуассона дает возможность определить потенциал поля объемных зарядов, если известно расположение этих зарядов.

1.1.13. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

       Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:

 - уравнение эквипотенциальной поверхности.

       При перемещении по эквипотенциальной поверхности на отрезок  потенциал не изменяется . Таким образом, касательная к поверхности составляющая вектора  равна нулю. Тогда вектор  направлен по нормали к эквипотенциальной поверхности в каждой ее точке, а линии напряженности в каждой точке перпендикулярны к эквипотенциальным поверхностям.

       Если эквипотенциальные поверхности построить таким образом, чтобы разность потенциалов для двух соседних поверхностей была одна и та же, то по густоте эквипотенциальных поверхностей можно судить о напряженности поля. Действительно, чем гуще эквипотенциальные поверхности, тем больше , тем больше .

       Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.

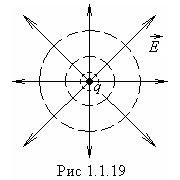
       Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.1.19)

.

Таким образом, эквипотенциальная поверхность этого заряда будет сферой радиуса  с центром в точке заряда. Силовые же линии, как мы установили ранее, расходятся радиально от заряда если он , или сходятся к заряду, если он “-”. То есть вектор  перпендикулярен эквипотенциальным поверхностям.

ЛЕКЦИЯ 5

1.2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ

1.2.1.ПОЛЯРНЫЕ И НЕПОЛЯРНЫЕ МОЛЕКУЛЫ

         Если диэлектрик внести в электрическое поле, то и поле, и диэлектрик претерпевают изменения. В составе атомов и молекул имеются положительные и отрицательные заряды (ядра, электроны). Электроны движутся в пределах атома или молекулы с огромной скоростью, их положения меняются, и действие каждого электрона на заряды будет таким, как если бы он находился в покое в некоторой точке, которая является усредненным положением электронов во времени.

           Если расстояния превышают размеры молекулы, то действие всех электронов молекулы эквивалентно действию суммарного заряда, помещенного в некоторую точку внутри молекулы. Эта точка называется центром тяжести отрицательных зарядов, Действие же ядер эквивалентно действию их суммарного заряда, по­мещенного в центр тяжести положительных зарядов. Ясно, что центр положительных зарядов определяется радиус-вектором: