Основы электростатики. Изучение электрического поля, страница 25

       Напряженность поля связанных зарядов отлична от нуля только внутри самого слоя диэлектрика. Вне конденсатора (при  и ) поля нет, , .

       Найдем напряженность поля в пространстве между пластинами . Выберем цилиндрическую гауссову поверхность, показанную на рис.1.2.10 штриховой линией. Образующие цилиндра параллельны оси , а основания параллельны заряженным плоскостям. Площадь каждого основания .

       Левое основание находится в области , где , а правое проходит через точку поля с координатой  , в которой вычисляется поле. Поток смещения через поверхность цилиндра равен потоку только через правое основание:

.

Внутри гауссовой поверхности  находится свободный заряд, размещенный на площадке  левой плоскости и равный . Тогда по теореме Гаусса

,

отсюда  .

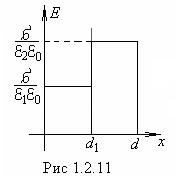
          В первом слое напряженность поля равна

 при .

             Во втором слое

 при ,

график зависимости  при  представлен на рис. 1.2.11.

3. Поле равномерно заряженной сферы радиуса , окруженной концентрическими слоями двух разных диэлектрических сред. Наружный радиус первой среды с относительной диэлектрической проницаемостью

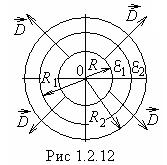 равен , а второй среды  равен  (рис. 1.2.12).

За пределами второй среды  - вакуум. Поверхностная плотность свободных зарядов на сфере радиуса  равна .

       Центр  заряженной сферы и концентрических слоев диэлектриков является центром симметрии поля. Поэтому в любой точке поля векторы  и  направлены радиально от центра , если , или к центру , если , то есть ; . Выберем в качестве гауссовой поверхности  сферу радиуса  с центром в  точке О.  Во всех точках этой поверхности , где  - проекция вектора  на радиус-вектор , проведенный из центра  в рассматриваемую точку поля на поверхности . Из симметрии поля следует, что во всех точках поверхности  значения  одинаковы.       Поэтому поток смещения через поверхность  равен: