Основы электростатики. Изучение электрического поля, страница 7

.

Векторы  и  взаимно перпендикулярны, поэтому результирующая напряженность  равна:

Таким образом, напряженность электростатического поля диполя зависит от направления радиус-вектора  относительно оси диполя и убывает пропорционально кубу расстояния  от его центра, то есть значительно быстрее, чем в случае поля одного точечного заряда.

                                                                     Лекция 3

1.1.6. ГУСТОТА ЛИНИЙ НАПРЯЖЕННОСТИ.  ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ

       Силовую линию поля (линию напряженности) можно провести через любую точку пространства, так что число проводимых линий ничем не ограничено. Линия напряженности в этом случае дает лишь направление напряженности и не характеризует ее величину. Однако можно ввести условие, связывающее величину напряженности с числом проводимых силовых линий. Тогда в местах, где напряженность больше, линии напряженности будут гуще.

       Электростатическое поле разобьем на малые области. В каждой такой области проведем площадку , перпендикулярную к линиям напряженности. Через площадку  проведем такое число  линий напряженности, чтобы число линий, приходящихся на единицу поверхности, было равно напряженности в области площадки , то есть потребуем, чтобы выполнялось условие:

.

       При выполнении этого условия величина напряженности оказывается связанной с густотой силовых линий. Общее число  линий, пронизывающих поверхность , равно потоку вектора  через эту поверхность:

;

где ,  - единичный вектор внешней нормали к поверхности .

1.1.7. ТЕОРЕМА ГАУССА

       Если известно расположение зарядов, то электрическое поле  зарядов можно найти по принципу суперпозиции. Однако применение этого метода в каждом отдельном случае требует довольно сложных вычислений. Задача может быть решена довольно просто применением некоторых теорем, которые мы здесь рассмотрим.

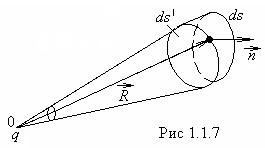
       Вычислим поток вектора  через бесконечно малую площадку . Будем считать, что поле создано точечным зарядом   в вакууме, находящимся в точке  (рис.1.1.7).

Из заряда  проведем радиус-вектор  к площадке . Тогда поток  вектора  через эту площадку будет равен: .

Произведение  равно проекции площадки  на поверхность, перпендикулярную к  . Это произведение положительно, если из  видна внутренняя сторона площадки  (угол  острый), и отрицательно, если видна ее внешняя сторона (угол тупой), то есть , где  - абсолютная величина перпендикулярной к  проекции площадки . Пусть  - телесный угол, под которым площадка  видна из точки . Тогда