Основы электростатики. Изучение электрического поля, страница 11

3.Рассмотрим электрическое поле, созданное двумя разноименно заряженными  плоскостями  с поверхностными плотностями заряда  и . Очевидно, напряженности полей плоскостей направлены в одну сторону (от положительной плоскости к отрицательной, рис.1.1.12), и результирующая напряженность , где  - напряженность поля одной заряженной плоскости. Окончательно получаем

4.Вычислим напряженность электрического поля, создаваемого заряженной сферой радиуса R. Заряд сферы q, его поверхностная плотность  Для определения напряженности построим гауссову поверхность в виде сферы радиуса r, центр которой совпадает с центром заряженной сферы (рис.1.1.13).

                При r≤R  внутри гауссовой поверхности зарядов нет, так как весь заряд распределен по поверхности сферы. По теореме Гаусса или  , следовательно,  - напряженность электрического поля внутри заряженной сферы равна нулю.

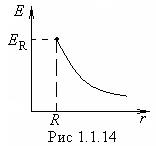
         При  внутрь гауссовой поверхности попадает весь заряд q  сферы. В силу центральной симметрии поля напряженность на расстоянии r от центра сферы всюду одинакова, и  или  при этом  , тогда , и   С ростом r значения Е убывают пропорционально (рис.1.1.14). На поверхности сферы напряженность испытывает скачек

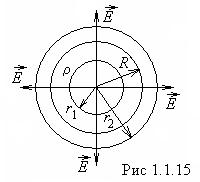
5.Рассмотрим электрическое поле, созданное объемно заряженным шаром радиуса R . Объемная плотность заряда шара ρ. Гауссову поверхность построим в виде сферы, центр которой совпадает с центром шара, а радиус равен r (рис.1.1.15).

                При внутрь гауссовой поверхности попадает заряд , тогда по теореме Гаусса , и . На поверхности шара при r=R напряженность .

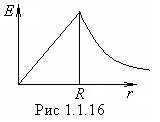
                При  внутрь гауссовой поверхности попадает весь заряд , и , отсюда  На поверхности сферы  т.е.  и скачка напряженности не происходит. Зависимость  представлена на рис1.1.16.

Лекция 4

1.1.9.ПОТЕНЦИАЛЬНЫЙ ХАРАКТЕР ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.РАБОТА СИЛ ПОЛЯ ПРИ ПЕРЕМЕЩЕНИИ ЗАРЯДОВ. ЦИРКУЛЯЦИЯ И РОТОР ВЕКТОРА НАПРЯЖЕННОСТИ

     Работа, совершаемая силами электростатического поля при перемещении заряда  на отрезок  равна: