Волновые процессы в материальных средах: Учебное пособие, страница 9

Приведем некоторые частные случаи тензора однородного напряжения: одноосное напряжение (линейно-напряженное состояние)

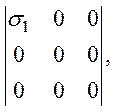
двуосное напряжение (плоско-напряженное состояние)

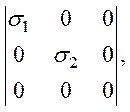
гидростатическое сжатие

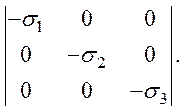
Обратим внимание на существенное отличие тензора механических напряжений от тех тензоров второго ранга, которыми описываются свойства кристалла, например, тензоров диэлектрической и магнитной проницаемости и т. п. Это материальные тензоры. Симметрия материальных тензоров и ориентировка их характеристической поверхности определяются симметрией кристалла. Тензор напряжений не описывает свойств кристалла и не связан с его симметрией. Он зависит только от внешней силы. Тензор механических напряжений − полевой тензор, или тензор воздействия.

Д е ф о р м а ц и и. Под влиянием приложенных сил твердые тела деформируются. Представим себе малую однородную трехмерную деформацию твердого тела. Пусть точка 0, соответствующая началу координат, сохранила свое положение, а все остальные точки тела в результате деформации изменили свои положения. Например, точка x (x₁, x₂, x₃) переместилась в положение (рис. 7).

Рис. 7. Смещение точки

Отрезок ΔUназовем смещением точки x. Очевидно, что

В твердом теле при малых деформациях компоненты смещения зависят от первоначального положения точки:

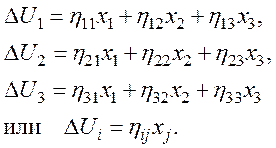
Девять компонент  образуют тензор 2-го ранга, называемый тензором деформаций.

Компоненты вектора  также являются функциями первоначального положения точки x:

или

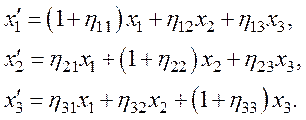
Чтобы пояснить физический смысл компонент тензора , рассмотрим частный случай, когда точка x₁ располагалась на оси x₁и в результате деформации переместилась в положение .

Тогда ,

откуда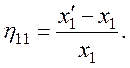

Компонента  определяет деформацию относительного удлинения (растяжения-сжатия) вдоль оси x₁. Аналогичный смысл имеют компоненты : деформации относительного растяжения-сжатия вдоль осей x₂ и x₃.

Рассмотрим теперь смещение той же точки вдоль оси x₂:

откуда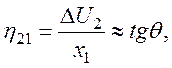

т. е. компонента  определяет поворот линейного элемента, параллельного оси x_i (поворот происходит вокруг третьей оси в сторону x_j).

Для того чтобы отделить собственно деформацию тела от его вращения как целого, тензор  делят на антисимметричную и симметричную части:

Антисимметричная часть 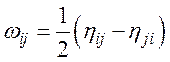 описывает вращение тела как целого и этот тензор антисимметричен.

Симметричный тензор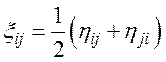

представляет собой собственно тензор деформаций:

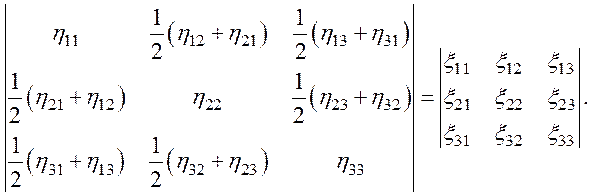
Диагональные компоненты ξ_ij описывают удлинения или сжатия вдоль оси i. Остальные компоненты ξ_ij − компоненты сдвига.

Подобно тензору напряжений, тензор деформаций не является материальным тензором. Только в случае теплового расширения тензор деформаций зависит от симметрии кристалла.

3.5. Упругие свойства. Закон Гука

Основным законом теории упругости твердых тел в области малых деформаций является закон Гука: деформация, возникающая в теле под действием силы, пропорциональна этой силе. Линейная связь между напряжением s_ij и деформацией ξ для твердых тел существует лишь в области малых деформаций (ξ<1%).

Если прекращается действие силы, упругие деформации и напряжения исчезают, форма тела полностью восстанавливается.

Для изотропных тел закон Гука выражается формулой:

ξ=Ss

или s=Cξ.

Здесь s− напряжение; ξ − деформация; S и C − величины, характеризующие упругие свойства твердого тела; C − жесткость (константа упругости, постоянная жесткости, или постоянная упругой жесткости); S − податливость, или упругий модуль (постоянная гибкости, модуль упругости, упругая податливость).

Термином «упругие постоянные» обозначают как величины C, так и величины S. В анизотропных телах напряжение характеризуется тензором s_kl, а деформация − тензором ξ_ij.

Каждая компонента тензора ξ_ij связана с каждой компонентой тензора s_kl соотношением

ξ₁₁=S₁₁₁₁s₁₁+S₁₁₁₂s₁₂+S₁₁₁₃s₁₃+S₁₁₂₁s₂₁+S₁₁₂₂s₂₂+S₁₁₂₃s₂₃+S₁₁₃₁s₃₁+S₁₁₃₂s₃₂+

        +S₁₁₃₃s₃₃  и т. д.

В каждое из девяти таких уравнений входит по девять коэффициентов S_ijkl, образующих тензор 4-го ранга, в матрице которого 81 компонента. Коэффициенты C_ijkl также образуют тензор 4-го ранга.

Закон Гука для кристаллов записывается в следующем виде:

s_ij=C_ijkξ_kl                                                                                                    (15)

или

ξ_ij=S_ijkls_kl                                                                                                           (16)

Уравнения (15) или (16) означают, что деформация кристалла зависит от направления и типа приложенного напряжения. Например, одноосное растягивающее напряжение, которое в изотропном теле вызвало бы только растяжение вдоль той же оси (и поперечное сокращение), в кристалле может вызвать растяжения, сжатия и сдвиги в любых направлениях в зависимости от того, какова симметрия этого кристалла.

Вследствие симметричности тензоров s_ij и ξ_ij, упругие модули S и C тоже симметричны, в том числе и по перестановке пар индексов, т. е. S_ijkl, C_ijkl. В результате действия симметрии число независимых компонент тензоров S и C сокращается до 21.

Внутренняя симметрия кристаллов приводит еще к значительному сокращению числа независимых компонент в указанных тензорах.

3.6. Физический смысл компонент упругих постоянных тензоров

Каждая компонента тензора S_mn определяет связь между определенными компонентами напряжений и деформаций S₁₁, S₂₂, S₃₃ связывают нормальные (растягивающие или сжимающие) напряжения с параллельными им деформациями продольного удлинения (растяжения-сжатия). Эти коэффициенты всегда больше нуля.

Коэффициенты S₁₂, S₁₃, S₂₃, S₂₁, S₃₁, S₃₂ определяют связь между нормальным напряжением и деформацией поперечного сжатия (или растяжения). Эти компоненты обычно меньше нуля.

Компоненты S₄₄, S₅₅, S₆₆ связывают напряжения сдвига (касательные) с деформацией сдвига, параллельного приложенному напряжению.

Компоненты S₂₄, S₃₄, S₃₅, S₁₅, S₁₆, S₂₆, S₅₁, S₆₁, S₆₂, S₄₂, S₄₃, S₅₃ связывают нормальные напряжения с деформациями сдвига в плоскости, параллельной напряжению, или деформацию растяжения-сжатия с параллельным ей касательным напряжением.