Волновые процессы в материальных средах: Учебное пособие, страница 17

Когда же заряженные частицы можно считать достаточно свободными, чтобы их совокупность обладала плазменными свойствами? Точный ответ дать сложно, однако энергетическим условием плазмоподобного поведения можно считать условие, когда колебательная или тепловая энергия частиц твердого тела составляет заметную часть кулоновской энергии, связывающей их в решетке. Это условие должно иметь вид

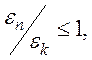
здесь ε_n – средняя потенциальная энергия взаимодействия между частицами; ε_k – их кинетическая энергия;

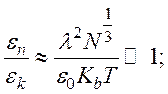
ε₀ –постоянная вакуума, равная .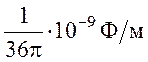

С учетом сложного взаимодействия частиц в твердом теле это соотношение имеет значение

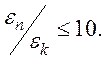                                                                                                    (76)

Если выполняется условие (76), то система частиц является плазмой, составляющие ее частицы свободно перемещаются одна относительно другой и дальний порядок отсутствует.

6. Длины экранирования

Характер поведения плазмы зависит от величины некоторой критической длины. Отклик плазмы будет коллективным для тех длин волн, которые больше критической длины; возмущения с более короткими длинами волн приводят к одночастичному отклику.

В классической плазме эта критическая длина называется дебаевским радиусом экранирования, а в вырожденной плазме – Томаса-Ферми. Эти критические длины – наиболее важные параметры, характеризующие плазму:

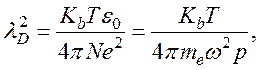                                                                                                    (77)

где К_b - постоянная Больцмана, К_b = 1,38×10^-28 Дж/град; T- абсолютная температура плазмы, градус Кельвина; e – заряд электрона =1,6×10^-19 Кл.;

N – концентрация носителей; ω_p - плазменная частота; 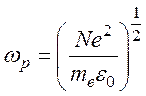– плазменная частота (Лэнгмюровская).

Определяемая соотношением (77) характерная длина имеет важный физический смысл. Это длина экранирования плазмы, т. е. расстояние, на которое проникает в плазму внешнее электростатическое поле, нейтрализуемое полями, индуцированными вследствие поляризации среды. Можно сказать, что среда не является плазмой, если она не экранирует внешнего электростатического поля.

В легированных полупроводниках значения радиусов экранирования находятся в пределах 10–10 см в зависимости от концентрации.

В металлах плазма гораздо более плотная и всегда вырождена. Типичное значение радиуса экранирования в металлеλ_D= см. Дебаевский радиус характеризует расстояние, на котором плазма экранирует себя от локального избытка заряда.

Пусть в плазму внесен пробный положительный заряд q (рис. 15). Расположенные по соседству электроны будут им притягиваться, а ионы, наоборот отталкиваться. В результате вокруг заряда возникает отрицательно заряженное сферически симметричное облако. Оно будет экранировать действие заряда на расположенную вокруг плазму. Ясно, что на некотором удалении от заряда поле будет исчезающе малым. Это расстояние и определяет радиус отрицательно заряженного облака.

Рис. 15. К определению понятия длины экранирования

7. Характерная частота.

Рассмотренные выше характерные длины разделяют область длин волн на две. В одной из них (λ>λ_D) отклик плазмы является коллективным, а в другой (λ<λ_D) ее поведение близко к одночастичному. Естественно поставить вопрос: существует ли подобное разделение во времени (частоте)? Да, существует.

Любая плазма имеет характерную частоту, называемую плазменной частотой, которая определяет характер отклика плазмы на изменяющееся во времени возмущение.

Плазменная частота – это частота основной моды коллективных колебаний заряженной среды, представляющая собой продольную волну плотности заряда.

Физическое происхождение плазменных колебаний можно объяснить следующим образом: возмущение плотности плазмы, которое вызывается каким-либо внешним воздействием, создает согласно уравнения Пуассона поле

где напряженность электростатического поля; n возмущение (изменение) плотности плазмы.

Это поле, в свою очередь, вызывает ток 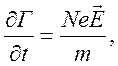 где – поток частиц в таком направлении, чтобы сгладить начальное возмущение. Однако из-за инерции электронов этот процесс приводит к «перелету»: области, первоначально заряженные отрицательно, приобретают положительный заряд и наоборот. Этот процесс повторяется и приводит к колебаниям, описываемым уравнением гармонического осциллятора

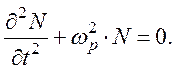
Возвращающая сила в рассматриваемых колебаниях возникает за счет кулоновского взаимодействия между электронами, обладающими инерцией.

Характерная частота этих колебаний 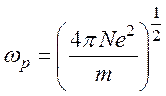– это плазменная или лэнгмюровская частота.

Частотаω_p разделяет высокочастотную и низкочастотную области, в которых плазма ведет себя различным образом.

Электрические поля с частотой меньшей, чем ω_p, экранируются, в то время как влияние плазмы на поля большей частоты незначительно, т.е. плазма отражает электромагнитные волны с частотами ниже ω_p, но пропускает более высокочастотные волны. Итак, при нарушении электронейтральности в какой-либо области плазмы в ней возникают гармонические колебания плотности заряда с частотой ω_p. Учет столкновений ионов и электронов (друг с другом и с нейтральными молекулами) приводит к затуханию плазменных колебаний. Отметим, что плазменные колебания не имеют волнового характера – нарушения электронейтральности не распространяются по плазме. Очевидно, что нарушения электронейтральности можно наблюдать только в течение промежутков времени . Это время является для плазмы характерным. На временах, превышающих τ_p, нарушения электронейтральности не проявляются. Для типичных полупроводников ω_p≈10¹², что соответствует миллиметровому диапазону длин волн.

8. Циклотронная частота.

Другой частотой, характерной для плазмы, помещенной в статическое магнитное поле , является циклотронная частота 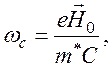 соответствующая угловой частоте спирального движения электронов вдоль магнитных силовых линий. Для полей порядка 10 кГс и m^*≈m, Гц

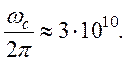
Наличие магнитного поля существенно изменяет отклик плазмы на низкочастотные (ω≤ω_c) возмущения. Влияние поля настолько велико, что делает возможным распространение низкочастотных электромагнитных волн, которые в отсутствие магнитного поля распространяться не могут.